指令集优化

指令集是指CPU能执行的所有指令的集合，每一指令对应一种操作，任何程序最终要编译成一条条指令才能让CPU识别并执行。CPU依靠指令来计算和控制系统，所以指令强弱是衡量CPU性能的重要指标，指令集也成为提高CPU效率的有效工具。

CPU都有一个基本的指令集，比如说目前英特尔和AMD的绝大部分处理器都使用的是X86指令集，因为它们都源自于X86架构。但无论CPU有多快，X86指令也只能一次处理一个数据，这样效率就很低下，毕竟在很多应用中，数据都是成组出现的，比如一个点的坐标（XYZ）和颜色（RGB）、多声道音频等。为了提高CPU在某些方面的性能，就必须增加一些特殊的指令满足时代进步的需求，这些新增的指令就构成了扩展指令集。该指令集采用单指令多数据(single instruction multiple data,简称 SIMD)扩展技术。

指令集查询网站：https://software.intel.com/sites/landingpage/IntrinsicsGuide/

汇编

最接近硬件的语言

MMX

MMX是由英特尔开发的一种**SIMD**多媒体指令集，共有57条指令。它于1996年集成在英特尔奔腾（Pentium）MMX处理器上，以提高其多媒体数据的处理能力。

其优点是增加了處理器關於多媒体方面的处理能力，缺点是占用浮点数寄存器进行运算（64位MMX寄存器实际上就是浮点数寄存器的别名）以至于MMX指令和浮点数操作不能同时工作。为了减少在MMX和浮点数模式切换之间所消耗的时间，程序员们尽可能减少模式切换的次数，也就是说，这两种操作在应用上是互斥的。AMD在此基础上发展出3D Now!指令集。

SSE

**SSE（Streaming SIMD Extensions）**是英特尔在AMD的3D Now!发布一年之后，在其计算机芯片Pentium III中引入的指令集，是繼MMX的擴充指令集。SSE指令集提供了70條新指令。AMD后来在Athlon XP中加入了对这个新指令集的支持。

SSE加入新的8個128位元暫存器（XMM0～XMM7）。而AMD發表的x86-64延伸架構（又稱AMD64）再加入額外8個暫存器。除此之外還有一個新的32位元的控制／狀態暫存器（MXCSR）。不過只能在64位元的模式下才能使用額外8個暫存器。

SSE（Streaming SIMD Extensions，流式单指令多数据扩展）指令集是1999年英特尔在Pentium III处理器中率先推出的，并将矢量处理能力从64位扩展到了128位。在Willamette核心的Pentium 4中英特尔又将扩展指令集升级到SSE2（2000年），而SSE3指令集（2004年）是从Prescott核心的Pentium 4开始出现。 SSE4（2007年）指令集是自SSE以来最大的一次指令集扩展，它实际上分成Penryn中出现的SSE4.1和Nehalem中出现的SSE4.2，其中SSE4.1占据了大部分的指令，共有47条，Nehalem中的SSE4指令集更新很少，只有7条指令，这样一共有54条指令，称为SSE4.2。

AVX

2007年8月，AMD抢先宣布了SSE5指令集(SSE到SSE4均为英特尔出品)，英特尔当即黑脸表示不支持SSE5，转而在2008年3月宣布Sandy Bridge微架构将引入全新的AVX指令集，同年4月英特尔公布AVX指令集规范，随后开始不断进行更新，业界普遍认为支持AVX指令集是Sandy Bridge最重要的进步，没有之一。 AVX（Advanced Vector Extensions，高级矢量扩展）指令集借鉴了一些AMD SSE5的设计思路，进行扩展和加强，形成一套新一代的完整SIMD指令集规范。

AVX高级矢量扩展，在SSE的基础上又把寄存器大小扩展为256bit。这次AVX将所有16个128位XMM寄存器扩充为256位的YMM寄存器，从而支持256位的矢量计算。理想状态下，浮点性能最高能达到前代的2倍水平。同时所有的SSE/SSE2/SSE3/SSSE3/SSE4指令是被AVX全面兼容的（AVX不兼容MMX），因此实际操作的是YMM寄存器的低128位，在这一点上与原来的SSE系列指令集无异。

  • 支持256位矢量计算，浮点性能最大提升2倍

  • 增强的数据重排，更有效存取数据

  • 支持3操作数和4操作数，在矢量和标量代码中能更好使用寄存器

  • 支持灵活的不对齐内存地址访问

  • 支持灵活的扩展性强的VEX编码方式，可减少代码

AVX2指令集将大多数整数命令操作扩展到256位，并引入了熔合乘法累积（FMA）运算。AVX-512则使用新的EVEX前缀编码将AVX指令进一步扩展到512位。Intel Xeon Scalable處理器支援AVX-512。

NEON

NEON是一种SIMD(Single Instruction Multiple Data)指令，也就是说，NEON可以把若干源(source)操作数(operand)打包放到一个源寄存器中，对他们执行相同的操作，产生若干目的(dest)操作数，这种方式也叫向量化(vectorization)。

可能你对这个描述还不够清晰，简单来说，就是：NEON指令优化的精髓就在于同时在不同通道内进行并行运算。通常可用于图像等矩阵数据的循环优化。

更简单的说，就是，将Neon寄存器分为多个通道，每个通道存储一个数据。一条对Neon寄存器的计算指令，实际上，是对各通道的数据分别的计算指令。即寄存器位宽，直接影响到数据的通道数。

例如：在ARMv7的NEON unit中，register file总大小是1024-bit，可以划分为16个128-bit的Q-register(Quadword register)或者32个64-bit的D-register(Dualword register)，也就是说，最长的寄存器位宽是128-bit。那么，假设我们采用32-bit单精度浮点数float来做浮点运算，那么可以把最多128/32=4个浮点数打包放到Q-register中做运算，即4个4个参与计算，从而提高吞吐量，减少loop次数。

neon指令集列表：https://gcc.gnu.org/onlinedocs/gcc-4.7.4/gcc/ARM-NEON-Intrinsics.html#ARM-NEON-Intrinsics

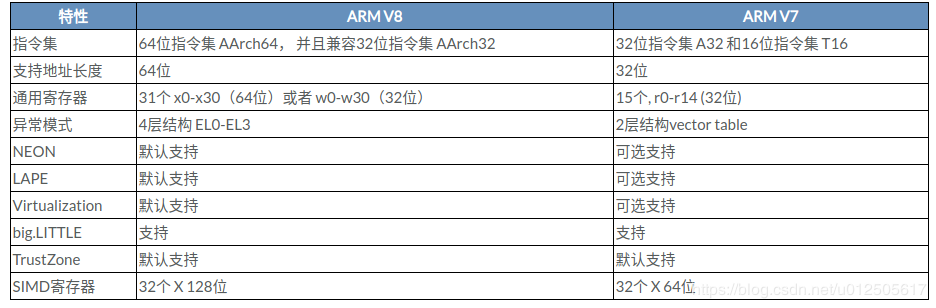
ARMv7 与 ARMv8的区别

arm_arch

指令集优化例子

汇编

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212

#ifdef __aarch64__
#include "MNNAsmGlobal.h"

.text
.align 5
asm_function MNNFloat16_Common_4_MatMul
//void MNNFloat16_Common_4_MatMul(int16_t* dst, const int16_t* src, const int16_t* weight, size_t icUnit, size_t ocUnit, size_t ocStep, size_t width);
//Auto: x0: dst, x1:src, x2:weight, x3:icUnit
//x4: ocUnit, x5:ocStep, x6: width

mov x12, #8 // 4*sizeof(__fp16)
mul x12, x6, x12

.macro COMPUTE z0 z1 z2 z3 z4 z5 z6 z7
        ld1 {v0.8h}, [x7], #16
        fmla \z0, v2.8h, v0.h[0]
        fmla \z1, v2.8h, v0.h[4]
        fmla \z0, v3.8h, v0.h[1]
        fmla \z1, v3.8h, v0.h[5]
        fmla \z0, v4.8h, v0.h[2]
        ld1 {v1.8h}, [x7], #16
        fmla \z1, v4.8h, v0.h[6]
        fmla \z0, v5.8h, v0.h[3]
        fmla \z1, v5.8h, v0.h[7]
        fmla \z2, v2.8h, v1.h[0]
        fmla \z3, v2.8h, v1.h[4]
        ld1 {v0.8h}, [x7], #16
        fmla \z2, v3.8h, v1.h[1]
        fmla \z3, v3.8h, v1.h[5]
        fmla \z2, v4.8h, v1.h[2]
        fmla \z3, v4.8h, v1.h[6]
        fmla \z2, v5.8h, v1.h[3]
        fmla \z3, v5.8h, v1.h[7]

        fmla \z4, v2.8h, v0.h[0]
        fmla \z5, v2.8h, v0.h[4]
        fmla \z4, v3.8h, v0.h[1]
        fmla \z5, v3.8h, v0.h[5]
        ld1 {v1.8h}, [x7], #16
        fmla \z4, v4.8h, v0.h[2]
        fmla \z5, v4.8h, v0.h[6]
        fmla \z4, v5.8h, v0.h[3]
        fmla \z5, v5.8h, v0.h[7]


        fmla \z6, v2.8h, v1.h[0]
        fmla \z7, v2.8h, v1.h[4]
        fmla \z6, v3.8h, v1.h[1]
        fmla \z7, v3.8h, v1.h[5]
        fmla \z6, v4.8h, v1.h[2]
        fmla \z7, v4.8h, v1.h[6]
        fmla \z6, v5.8h, v1.h[3]
        fmla \z7, v5.8h, v1.h[7]
.endm


L16:
cmp w6, #16
blt L8

mov x13, x2
mov x14, x0
mov x15, x1

mov x11, x4

LoopOzL16:
    movi v31.8h, #0
    movi v30.8h, #0
    movi v29.8h, #0
    movi v28.8h, #0
    movi v27.8h, #0
    movi v26.8h, #0
    movi v25.8h, #0
    movi v24.8h, #0

    movi v23.8h, #0
    movi v22.8h, #0
    movi v21.8h, #0
    movi v20.8h, #0
    movi v19.8h, #0
    movi v18.8h, #0
    movi v17.8h, #0
    movi v16.8h, #0

    mov x7, x1
    mov x8, x3
    mov x9, x14
    LoopSz16:
        ld1 {v2.8h, v3.8h}, [x2], #32
        ld1 {v4.8h, v5.8h}, [x2], #32

        COMPUTE v16.8h, v17.8h, v18.8h, v19.8h, v20.8h, v21.8h, v22.8h, v23.8h
        COMPUTE v24.8h, v25.8h, v26.8h, v27.8h, v28.8h, v29.8h, v30.8h, v31.8h

        sub x7, x7, #128
        add x7, x7, x12

        subs x8, x8, #1
        bne LoopSz16

    subs x11, x11, #1

    st1 {v16.8h, v17.8h, v18.8h, v19.8h}, [x9], #64
    st1 {v20.8h, v21.8h, v22.8h, v23.8h}, [x9], #64
    st1 {v24.8h, v25.8h, v26.8h, v27.8h}, [x9], #64
    st1 {v28.8h, v29.8h, v30.8h, v31.8h}, [x9], #64

    add x14, x14, x5
    bne LoopOzL16

sub w6, w6, #16
add x0, x0, #256 // 16*8*sizeof(float16)
add x1, x1, #128 // 16*4*sizeof(float16)
mov x2, x13

L8:
cmp w6, #8
blt L1

mov x13, x2
mov x14, x0
mov x15, x1

mov x11, x4

LoopOzL8:
    movi v23.8h, #0
    movi v22.8h, #0
    movi v21.8h, #0
    movi v20.8h, #0
    movi v19.8h, #0
    movi v18.8h, #0
    movi v17.8h, #0
    movi v16.8h, #0

    mov x7, x1
    mov x8, x3
    mov x9, x14
    LoopSz8:
        ld1 {v2.8h, v3.8h}, [x2], #32
        ld1 {v4.8h, v5.8h}, [x2], #32

        COMPUTE v16.8h, v17.8h, v18.8h, v19.8h, v20.8h, v21.8h, v22.8h, v23.8h
        sub x7, x7, #64
        add x7, x7, x12

        subs x8, x8, #1
        bne LoopSz8

    subs x11, x11, #1

    st1 {v16.8h, v17.8h, v18.8h, v19.8h}, [x9], #64
    st1 {v20.8h, v21.8h, v22.8h, v23.8h}, [x9], #64

    add x14, x14, x5
    bne LoopOzL8


add x0, x0, #128 // 8*8*sizeof(float16)
add x1, x1, #64 // 8*4*sizeof(float16)
mov x2, x13
sub w6, w6, #8

L1:
cmp w6, #0
beq End

LoopL1:
    mov x13, x2
    mov x14, x0
    mov x15, x1

    mov x11, x4

    LoopOzL1:
        movi v16.8h, #0
        movi v17.8h, #0

        mov x7, x1
        mov x8, x3
        mov x9, x14
        LoopSz1:
            ld1 {v2.8h, v3.8h}, [x2], #32
            ld1 {v4.8h, v5.8h}, [x2], #32

            ld1 {v0.4h}, [x7], x12
            fmla v16.8h, v2.8h, v0.h[0]
            fmla v17.8h, v3.8h, v0.h[1]
            fmla v16.8h, v4.8h, v0.h[2]
            fmla v17.8h, v5.8h, v0.h[3]

            subs x8, x8, #1
            bne LoopSz1
        fadd v16.8h, v16.8h, v17.8h
        subs x11, x11, #1
        st1 {v16.8h}, [x9], #16
        add x14, x14, x5
        bne LoopOzL1

    subs w6, w6, #1
    add x0, x0, #16 // 8*sizeof(float16)
    add x1, x1, #8 // 4*sizeof(float16)
    mov x2, x13
    bne LoopL1

End:

ret

#endif

neon

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77

void Matrix::multi(Tensor* C, const Tensor* A, const Tensor* B) {
    MNN_ASSERT(NULL != C);
    MNN_ASSERT(NULL != B);
    MNN_ASSERT(NULL != A);

    MNN_ASSERT(2 == C->dimensions());
    MNN_ASSERT(2 == B->dimensions());
    MNN_ASSERT(2 == A->dimensions());

    const auto a = A->host<float>();
    const auto b = B->host<float>();
    auto c       = C->host<float>();

    const int h = A->length(0);
    const int k = A->length(1);
    const int w = B->length(1);

    const int aw = A->stride(0);
    const int bw = B->stride(0);
    const int cw = C->stride(0);

    MNN_ASSERT(k == B->length(0));

    int y = 0;
    for (; y < h; ++y) {
        int x            = 0;
        const auto aLine = a + y * aw;
        auto cLine       = c + y * cw;
#ifdef MNN_USE_NEON
        // firstly, compute 16 together
        for (; x <= w - 16; x += 16) {
            auto bColumn     = b + x;
            float32x4_t sum0 = vdupq_n_f32(0.0);
            float32x4_t sum1 = vdupq_n_f32(0.0);
            float32x4_t sum2 = vdupq_n_f32(0.0);
            float32x4_t sum3 = vdupq_n_f32(0.0);
            for (int i = 0; i < k; ++i) {
                const auto bLine = bColumn + i * bw;
                float32x4_t a0   = vdupq_n_f32(aLine[i]);
                float32x4_t b0   = vld1q_f32(bLine);
                float32x4_t b1   = vld1q_f32(bLine + 4);
                float32x4_t b2   = vld1q_f32(bLine + 8);
                float32x4_t b3   = vld1q_f32(bLine + 12);
                sum0             = vmlaq_f32(sum0, a0, b0);
                sum1             = vmlaq_f32(sum1, a0, b1);
                sum2             = vmlaq_f32(sum2, a0, b2);
                sum3             = vmlaq_f32(sum3, a0, b3);
            }
            vst1q_f32(cLine + x, sum0);
            vst1q_f32(cLine + x + 4, sum1);
            vst1q_f32(cLine + x + 8, sum2);
            vst1q_f32(cLine + x + 12, sum3);
        }
        // secondly, compute 4 together
        for (; x <= w - 4; x += 4) {
            auto bColumn    = b + x;
            float32x4_t sum = vdupq_n_f32(0.0);
            for (int i = 0; i < k; ++i) {
                const auto bLine = bColumn + i * bw;
                float32x4_t a4   = vdupq_n_f32(aLine[i]);
                float32x4_t b4   = vld1q_f32(bLine);
                sum              = vmlaq_f32(sum, a4, b4);
            }
            vst1q_f32(cLine + x, sum);
        }
#endif
        for (; x < w; ++x) {
            auto bColumn = b + x;
            float sum    = 0.0f;
            for (int i = 0; i < k; ++i) {
                sum += aLine[i] * bColumn[i * bw];
            }
            cLine[x] = sum;
        }
    }
}

SSE

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

void _SSE_MNNMatrixAdd(float* C, const float* A, const float* B, size_t widthC4, size_t cStride, size_t aStride,
                  size_t bStride, size_t height) {
    for (int y = 0; y < height; ++y) {
        auto a = A + aStride * y;
        auto b = B + bStride * y;
        auto c = C + cStride * y;
        for (int x = 0; x < widthC4; ++x) {
            _mm_store_ps(c + 4 * x, _mm_add_ps(_mm_load_ps(b + 4 * x), _mm_load_ps(a + 4 * x)));
        }
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83

void _SSE_MNNGemmFloatCommon_4(float* dst, const float* src, const float* weight, size_t src_depth_quad, size_t dst_step,
                          size_t dst_depth_quad, size_t width, size_t weight_depth_offset) {
    auto src_depth_step = 4 * width;
    int wC4             = width / 4;
    int w4End           = wC4 * 4;
    for (int dz = 0; dz < dst_depth_quad; ++dz) {
        float* dst_z   = dst + dz * dst_step;
        auto weight_dz = weight + dz * (src_depth_quad * 16 + weight_depth_offset);

        for (int dx = 0; dx < wC4; ++dx) {
            float* dst_x        = dst_z + dx * 4 * 4;
            auto dst0           = _mm_set1_ps(0.0f);
            auto dst1           = _mm_set1_ps(0.0f);
            auto dst2           = _mm_set1_ps(0.0f);
            auto dst3           = _mm_set1_ps(0.0f);
            const float* src_dx = src + 4 * dx * 4;
            for (int sz = 0; sz < src_depth_quad; ++sz) {
                const float* src_z    = src_dx + sz * src_depth_step;
                const float* weight_z = weight_dz + sz * 16;
                auto w0               = _mm_loadu_ps(weight_z + 4 * 0);
                auto w1               = _mm_loadu_ps(weight_z + 4 * 1);
                auto w2               = _mm_loadu_ps(weight_z + 4 * 2);
                auto w3               = _mm_loadu_ps(weight_z + 4 * 3);
#define SSE_COMPUTE(v)                                   \
    {                                                \
        const float* srcValue = src_z + 4 * v;       \
        auto s0       = _mm_set1_ps(srcValue[0]);    \
        auto s1       = _mm_set1_ps(srcValue[1]);    \
        auto s2       = _mm_set1_ps(srcValue[2]);    \
        auto s3       = _mm_set1_ps(srcValue[3]);    \
        auto sw0      = _mm_mul_ps(s0, w0);          \
        auto sw1      = _mm_mul_ps(s1, w1);          \
        auto sw2      = _mm_mul_ps(s2, w2);          \
        auto sw3      = _mm_mul_ps(s3, w3);          \
        dst##v        = _mm_add_ps(dst##v, sw0);     \
        dst##v        = _mm_add_ps(dst##v, sw1);     \
        dst##v        = _mm_add_ps(dst##v, sw2);     \
        dst##v        = _mm_add_ps(dst##v, sw3);     \
    }

                SSE_COMPUTE(0);
                SSE_COMPUTE(1);
                SSE_COMPUTE(2);
                SSE_COMPUTE(3);
            }

            _mm_store_ps(dst_x + 4 * 0, dst0);
            _mm_store_ps(dst_x + 4 * 1, dst1);
            _mm_store_ps(dst_x + 4 * 2, dst2);
            _mm_store_ps(dst_x + 4 * 3, dst3);
        }

        for (int dx = w4End; dx < width; ++dx) {
            float* dst_x  = dst_z + dx * 4;
            auto dstValue = _mm_set1_ps(0.0f);

            const float* src_dx = src + 4 * dx;
            for (int sz = 0; sz < src_depth_quad; ++sz) {
                const float* src_z    = src_dx + sz * src_depth_step;
                const float* weight_z = weight_dz + sz * 16;
                auto w0               = _mm_loadu_ps(weight_z + 4 * 0);
                auto w1               = _mm_loadu_ps(weight_z + 4 * 1);
                auto w2               = _mm_loadu_ps(weight_z + 4 * 2);
                auto w3               = _mm_loadu_ps(weight_z + 4 * 3);

                auto s0       = _mm_set1_ps(src_z[0]);
                auto s1       = _mm_set1_ps(src_z[1]);
                auto s2       = _mm_set1_ps(src_z[2]);
                auto s3       = _mm_set1_ps(src_z[3]);

                auto sw0 = _mm_mul_ps(s0, w0);
                auto sw1 = _mm_mul_ps(s1, w1);
                auto sw2 = _mm_mul_ps(s2, w2);
                auto sw3 = _mm_mul_ps(s3, w3);
                dstValue = _mm_add_ps(dstValue, sw0);
                dstValue = _mm_add_ps(dstValue, sw1);
                dstValue = _mm_add_ps(dstValue, sw2);
                dstValue = _mm_add_ps(dstValue, sw3);
            }
            _mm_store_ps(dst_x, dstValue);
        }
    }
}

avx

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84

void _AVX_MNNGemmFloatCommon_4(float* dst, const float* src, const float* weight, size_t src_depth_quad, size_t dst_step,
                          size_t dst_depth_quad, size_t width, size_t weight_depth_offset) {
    auto src_depth_step = 4 * width;
    int wC8             = width / 8;
    int w8End           = wC8 * 8;
    for (int dz = 0; dz < dst_depth_quad; ++dz) {
        float* dst_z   = dst + dz * dst_step;
        auto weight_dz = weight + dz * (src_depth_quad * 16 + weight_depth_offset);

        for (int dx = 0; dx < wC8; ++dx) {
            float* dst_x        = dst_z + dx * 8 * 4;
            auto dst0           = _mm256_set1_ps(0.0f);
            auto dst1           = _mm256_set1_ps(0.0f);
            auto dst2           = _mm256_set1_ps(0.0f);
            auto dst3           = _mm256_set1_ps(0.0f);
            const float* src_dx = src + 8 * dx * 4;
            for (int sz = 0; sz < src_depth_quad; ++sz) {
                const float* src_z    = src_dx + sz * src_depth_step;
                const float* weight_z = weight_dz + sz * 16;
                auto w0               = _mm256_broadcast_ps((const __m128 *)(weight_z + 4 * 0));
                auto w1               = _mm256_broadcast_ps((const __m128 *)(weight_z + 4 * 1));
                auto w2               = _mm256_broadcast_ps((const __m128 *)(weight_z + 4 * 2));
                auto w3               = _mm256_broadcast_ps((const __m128 *)(weight_z + 4 * 3));
#define AVX_COMPUTE(v)                                   \
    {                                                \
        auto srcValue = _mm256_loadu_ps(src_z + 8 * v); \
        auto s0       = _mm256_shuffle_ps(srcValue, srcValue, _MM_SHUFFLE(0, 0, 0, 0)); \
        auto s1       = _mm256_shuffle_ps(srcValue, srcValue, _MM_SHUFFLE(1, 1, 1, 1)); \
        auto s2       = _mm256_shuffle_ps(srcValue, srcValue, _MM_SHUFFLE(2, 2, 2, 2)); \
        auto s3       = _mm256_shuffle_ps(srcValue, srcValue, _MM_SHUFFLE(3, 3, 3, 3)); \
        auto sw0      = _mm256_mul_ps(s0, w0);          \
        auto sw1      = _mm256_mul_ps(s1, w1);          \
        auto sw2      = _mm256_mul_ps(s2, w2);          \
        auto sw3      = _mm256_mul_ps(s3, w3);          \
        dst##v        = _mm256_add_ps(dst##v, sw0);     \
        dst##v        = _mm256_add_ps(dst##v, sw1);     \
        dst##v        = _mm256_add_ps(dst##v, sw2);     \
        dst##v        = _mm256_add_ps(dst##v, sw3);     \
    }

                AVX_COMPUTE(0);
                AVX_COMPUTE(1);
                AVX_COMPUTE(2);
                AVX_COMPUTE(3);
            }

            _mm256_storeu_ps(dst_x + 8 * 0, dst0);
            _mm256_storeu_ps(dst_x + 8 * 1, dst1);
            _mm256_storeu_ps(dst_x + 8 * 2, dst2);
            _mm256_storeu_ps(dst_x + 8 * 3, dst3);
        }
        _mm256_zeroall();

        for (int dx = w8End; dx < width; ++dx) {
            float* dst_x  = dst_z + dx * 4;
            auto dstValue = _mm_set1_ps(0.0f);

            const float* src_dx = src + 4 * dx;
            for (int sz = 0; sz < src_depth_quad; ++sz) {
                const float* src_z    = src_dx + sz * src_depth_step;
                const float* weight_z = weight_dz + sz * 16;
                auto w0               = _mm_loadu_ps(weight_z + 4 * 0);
                auto w1               = _mm_loadu_ps(weight_z + 4 * 1);
                auto w2               = _mm_loadu_ps(weight_z + 4 * 2);
                auto w3               = _mm_loadu_ps(weight_z + 4 * 3);

                auto s0       = _mm_set1_ps(src_z[0]);
                auto s1       = _mm_set1_ps(src_z[1]);
                auto s2       = _mm_set1_ps(src_z[2]);
                auto s3       = _mm_set1_ps(src_z[3]);

                auto sw0 = _mm_mul_ps(s0, w0);
                auto sw1 = _mm_mul_ps(s1, w1);
                auto sw2 = _mm_mul_ps(s2, w2);
                auto sw3 = _mm_mul_ps(s3, w3);
                dstValue = _mm_add_ps(dstValue, sw0);
                dstValue = _mm_add_ps(dstValue, sw1);
                dstValue = _mm_add_ps(dstValue, sw2);
                dstValue = _mm_add_ps(dstValue, sw3);
            }
            _mm_store_ps(dst_x, dstValue);
        }
    }
}

内存布局

减少缓存miss，提升处理效率。对内存的重新组织（Repacking）可以改进高速缓存命中率，从而提高性能。但是这种重新组织也是有开销的。

计算核中最小的计算单元处理的是两个 4×4 矩阵相乘。传统的方法由于 𝐾 可能很大，需要对输入内存进行重新组织，防止相邻的访存引起高速缓存冲突

quantization

量化将网络中主要算子（卷积）由原先的浮点计算转成低精度的Int8计算，减少模型大小并提升性能。

编译MNN时开启MNN_BUILD_QUANTOOLS宏，即开启量化工具的编译。

卷积优化

im2col

https://www.jianshu.com/p/4907e6c93452

空间换时间方案，重复放数据，提高cache命中率，以此提高运行速度，但比较浪费内存

im2col 是计算机视觉领域中将图片的不同通道（channel）转换成矩阵的列（column）的计算过程。Caffe 在计算卷积时，首先用 im2col 将输入的三维数据转换成二维矩阵，使得卷积计算可表示成两个二维矩阵相乘，从而充分利用已经优化好的 GEMM 库来为各个平台加速卷积计算。

图十二是卷积的 im2col 过程的示例。随着卷积过滤器在输入上滑动，将被使用的那部分输入展开成一行大小为 𝐼𝐶×𝐾𝐻×𝐾𝑊 的向量。在滑动结束后，则得到特征矩阵 (𝐻×𝑊)×(𝐼𝐶×𝐾𝐻×𝐾𝑊) 。将过滤器展开成 (𝑂𝐶)×(𝐼𝐶×𝐾𝐻×𝐾𝑊) 的矩阵，那么卷积即可表示成这两个矩阵相乘的结果（特征矩阵要进行转置操作）。

mnn_im2col

Winograd

https://arxiv.org/pdf/1509.09308.pdf

对于现代的CPU，加减乘除都可以在一个指令周期内完成，这种单纯减少乘法的变换（加法会增多），究竟有多少的价值，有待商榷？？论文测试系统是在GPU上实现的，GPU算乘法确实比加法要慢一些，比较适合本算法

https://www.cnblogs.com/shine-lee/p/10906535.html

Winograd快速卷积算法

fft

对于尺寸较大的卷积核，可以先fft变换为频域，相加后再反变换回来加速。

矩阵相乘 - strassen算法

典型矩阵乘法的复杂度是Θ(n^3)，采用分治的思想，可以降为Θ(nlog7) =Θ (n2.81)

matrix_strassen

矩阵乘法中采用分治法，第一感觉上应该能够有效的提高算法的效率。如上图所示分治法方案，以及对该算法的效率分析。有图可知，算法效率是Θ(n^3)。算法效率并没有提高。

鉴于上面的分治法方案无法有效提高算法的效率，要想提高算法效率，由主定理方法可知必须想办法将2中递归式中的系数8减少。Strassen提出了一种将系数减少到7的分治法方案，如下图所示。

matrix_strassen2

效率分析如下：

matrix_strassen3

性能分析

矩阵大小 朴素矩阵算法（秒） Strassen算法（秒）
32 0.003 0.003
64 0.004 0.004
128 0.021 0.071
256 0.09 0.854
512 0.782 6.408
1024 8.908 52.391

可以发现：可以看到使用Strassen算法时，耗时不但没有减少，反而剧烈增多，在n=512时计算时间就无法忍受，效果没有朴素矩阵算法好。网上查阅资料，现罗列如下：

1）采用Strassen算法作递归运算，需要创建大量的动态二维数组，其中分配堆内存空间将占用大量计算时间，从而掩盖了Strassen算法的优势。

2）于是对Strassen算法做出改进，设定一个界限。当n<界限时，使用普通法计算矩阵，而不继续分治递归。需要合理设置界限，不同环境（硬件配置）下界限不同。

3）矩阵乘法一般意义上还是选择的是朴素的方法，只有当矩阵变稠密，而且矩阵的阶数很大时，才会考虑使用Strassen算法。

GPU加速

本质上是类似的，都是GPU计算方案，只是底层API存在差异。

ios/mac osx：metal

opencl/opengl/vulken：android，linux，windows

opengl

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66

GLConvolutionIm2col::GLConvolutionIm2col(const std::vector<Tensor *> &inputs, const Op *convOp, Backend *bn) : GPUConvolution(convOp, bn) {
    auto totalWeightSize = ALIGN_UP4(mCommon->outputCount()) * ALIGN_UP4(mInputDepth) * (mCommon->kernelY() * mCommon->kernelX());
    mGLBackend = (GLBackend *)bn;
    auto mKernelBuffer = std::shared_ptr<GLSSBOBuffer>(new GLSSBOBuffer(sizeof(float) * totalWeightSize));
    int fw                = mCommon->kernelX();
    int fh                = mCommon->kernelY();
    mIsConv1x1 = (fw == 1 && fh == 1) ? true : false;
    int oc_4         = UP_DIV(mCommon->outputCount(), UNIT);
    int ic_4      = UP_DIV(mInputDepth, UNIT);
    float *dest           = (float *)mKernelBuffer->map(GL_MAP_WRITE_BIT | GL_MAP_INVALIDATE_BUFFER_BIT);
    if(NULL != dest){
        ::memset(dest, 0, totalWeightSize * sizeof(float));
        const float *source = convOp->main_as_Convolution2D()->weight()->data();
        int cur             = 0;

        //weight : oc ic -> oc/4 ic/4 ic4 oc4
        //weight image : oc_4, ic_4 * ic4 oc4
        int alignedWeightSize = ic_4 * fw * fh * UNIT2;
        for (int b = 0; b < mCommon->outputCount(); ++b) {
            int b_4      = b / UNIT;
            float *dst_b = dest + b_4 * alignedWeightSize;
            int mx       = b % UNIT;
            for (int d = 0; d < mInputDepth; ++d) {
                int my       = d % UNIT;
                int d_4      = d / UNIT;
                float *dst_d = dst_b + d_4 * fw * fh * UNIT2;
                for (int y = 0; y < fh; ++y) {
                    float *dst_y = dst_d + y * fw * UNIT2;
                    for (int x = 0; x < fw; ++x) {
                        float *dst_x          = dst_y + x * UNIT2;
                        dst_x[UNIT * my + mx] = source[cur++];
                    }
                }
            }
        }
    }else{
        MNN_ASSERT(NULL != dest);
    }

    mKernelBuffer->unmap();

    mKernelTexture = std::shared_ptr<GLTexture>(new GLTexture(ic_4 * UNIT*fw*fh, oc_4, 1, ((GLBackend *)backend())->getTextrueFormat(), GL_TEXTURE_2D, false));
    auto transform = mGLBackend->getProgram("transform_kernel_image", glsl_kernel2image_glsl);
    int imageWidth = ROUND_UP(mInputDepth, 4)*fw*fh;
    int imageHeight = oc_4;
    transform->useProgram();
    glBindImageTexture(0, mKernelTexture->id(), 0, GL_TRUE, 0, GL_WRITE_ONLY, ((GLBackend *)backend())->getTextrueFormat());
    glBindBufferBase(GL_SHADER_STORAGE_BUFFER, 2, mKernelBuffer->getId());
    OPENGL_CHECK_ERROR;
    glUniform1i(3, imageWidth);
    OPENGL_CHECK_ERROR;
    glUniform1i(4, imageHeight);
    OPENGL_CHECK_ERROR;
    ((GLBackend *)backend())->compute(UP_DIV(imageWidth, 4), UP_DIV(oc_4, 4), 1);
    OPENGL_CHECK_ERROR;

//bias
    mBiasBuffer.reset(new GLSSBOBuffer(sizeof(float) * ALIGN_UP4(mCommon->outputCount())));
    float* bias = (float*)(mBiasBuffer->map(GL_MAP_WRITE_BIT | GL_MAP_INVALIDATE_BUFFER_BIT));
    if(bias != nullptr){
        ::memset(bias, 0, ALIGN_UP4(mCommon->outputCount()) * sizeof(float));
        ::memcpy(bias, convOp->main_as_Convolution2D()->bias()->data(),
                 convOp->main_as_Convolution2D()->bias()->size() * sizeof(float));
    }
    mBiasBuffer->unmap();
}