背景

反向传播算法的核心是按照梯度下降的方向更新参数，从而取得函数的局部极小值（不能保证获得最优解）。

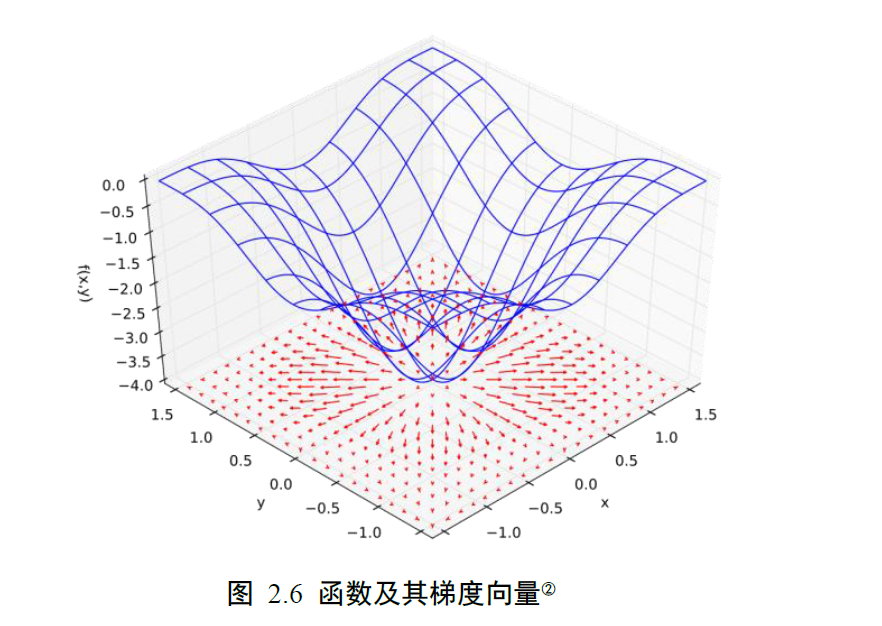
误差函数，激励函数的表达式可能很复杂，公式推导起来异常复杂，如何计算梯度就变得很关键。tensorflow为此引入了自动梯度计算工具，大大简化了梯度的计算过程，让人们从复杂的推导中解放出来。

常见方法

参见 https://blog.csdn.net/aws3217150/article/details/70214422

• 手动计算：纯手工推导实现，步骤复杂，参数一修改就得重新算。
• 数值微分：根据微分公式，带入极小的dx计算，计算量特别大，主要用于验证梯度计算。
• 符号微分：得能写成完整数学表达式，根据数学推导公式计算，容易出现表达式膨胀。况且AI计算并不关心导数的表达式，只关心最终的数值。
• 自动微分法：自动微分法是一种介于符号微分和数值微分的方法：数值微分强调一开始直接代入数值近似求解；符号微分强调直接对代数进行求解，最后才代入问题数值；自动微分将符号微分法应用于最基本的算子，比如常数，幂函数，指数函数，对数函数，三角函数等，然后代入数值，保留中间结果，最后再应用于整个函数。因此它应用相当灵活，可以做到完全向用户隐藏微分求解过程，由于它只对基本函数或常数运用符号微分法则，所以它可以灵活结合编程语言的循环结构，条件结构等，使用自动微分和不使用自动微分对代码总体改动非常小，并且由于它的计算实际是一种图计算，可以对其做很多优化，这也是为什么该方法在现代深度学习系统中得以广泛应用。

考虑如下函数 $$ f(x 1 ​ ,x 2 ​ )=ln(x 1 ​ )+x 1 ​ x 2 ​ −sin(x 2 ​ ) $$ 可以将其转化为如下计算图：

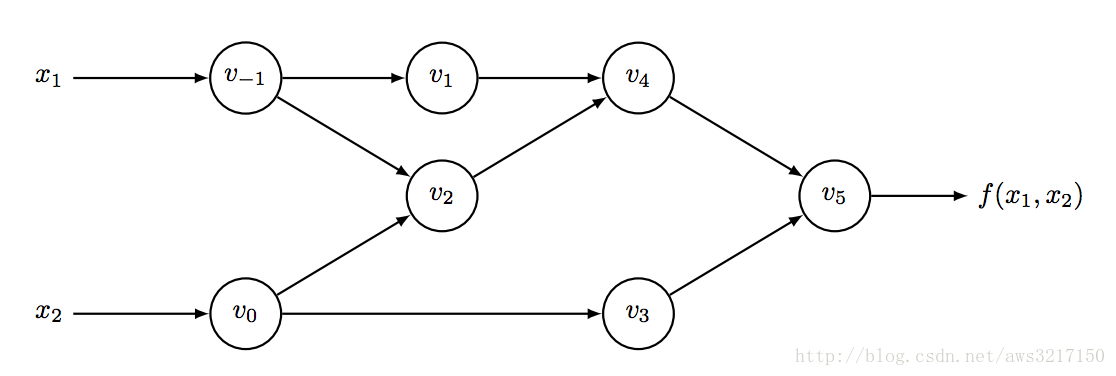
转化成如上DAG（有向无环图）结构之后，我们可以很容易分步计算函数的值，并求取它每一步的导数值：

神经网络一般输入特别大，输出很小，这样计算的话，计算量特别大，所以一般采用反向计算方式。

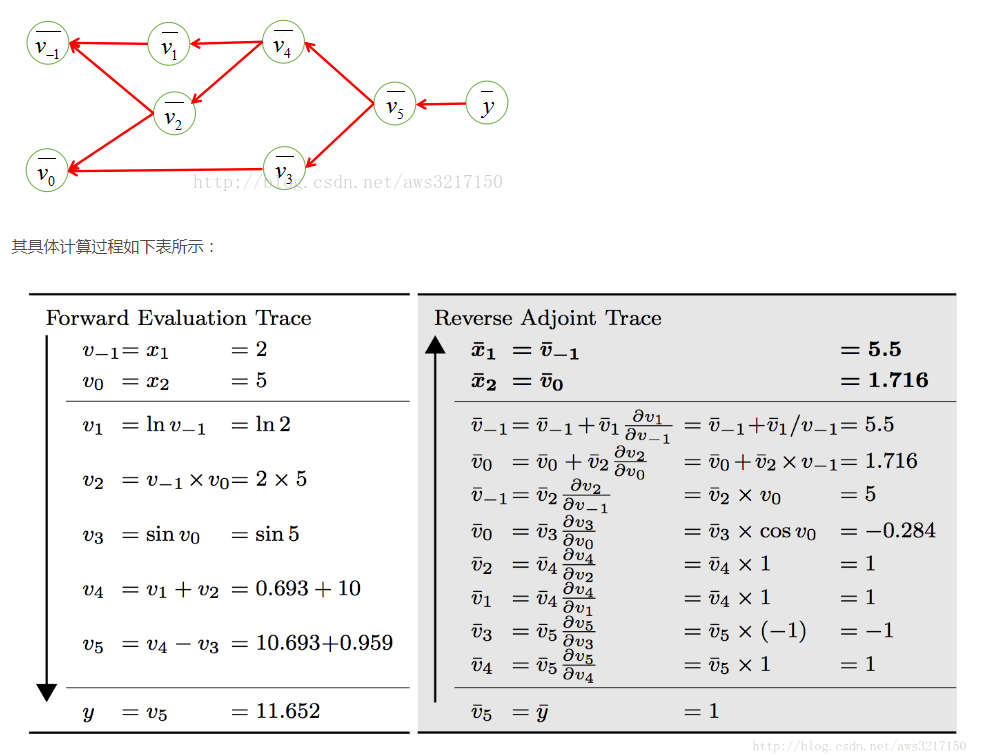
上述过程其实就是常见的链式求导过程。

vo，v-1存在2个输入，所以要计算多次。

反向算法计算一次就可以算出所有的梯度，大大提升了效率。

tensorflow实现

自动微分会将问题转化成一种有向无环图，因此我们必须构造基本的图部件，包括节点和边。可以先看看节点是如何实现的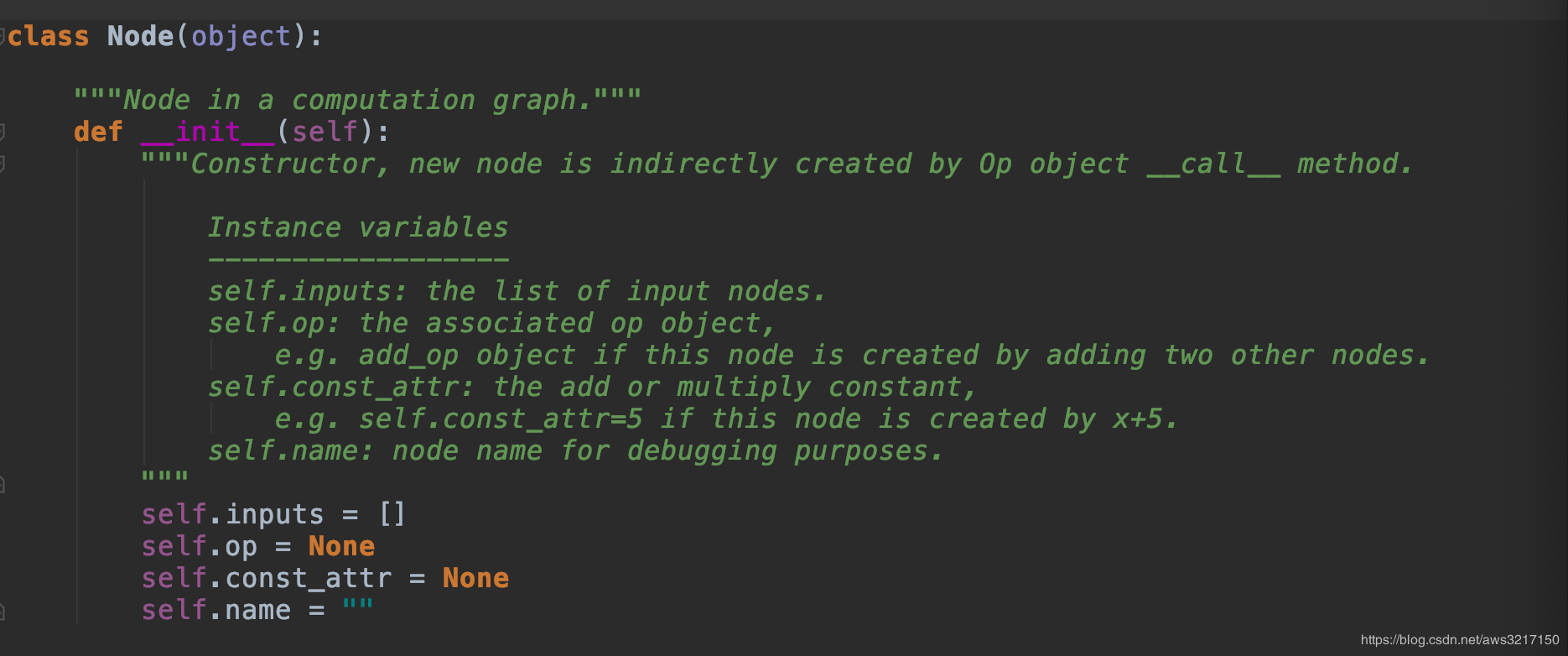： 首先节点可以分为三种：

• 常数节点
• 变量节点
• 带操作算子节点

因此Node类中定义了op成员用于存储节点的操作算子，const_attr代表节点的常数值，name是节点的标识，主要用于调试。对于边的实现则简单的多，每个节点只要知道本身的输入节点即可，因此用inputs来描述节点的关系。

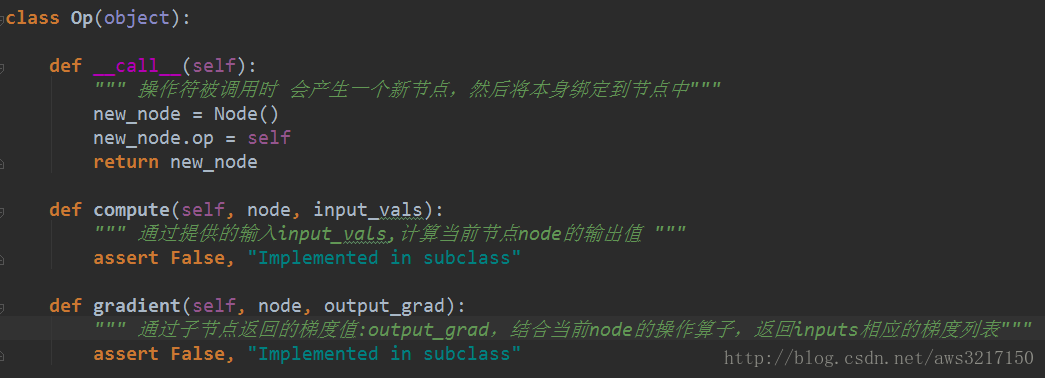
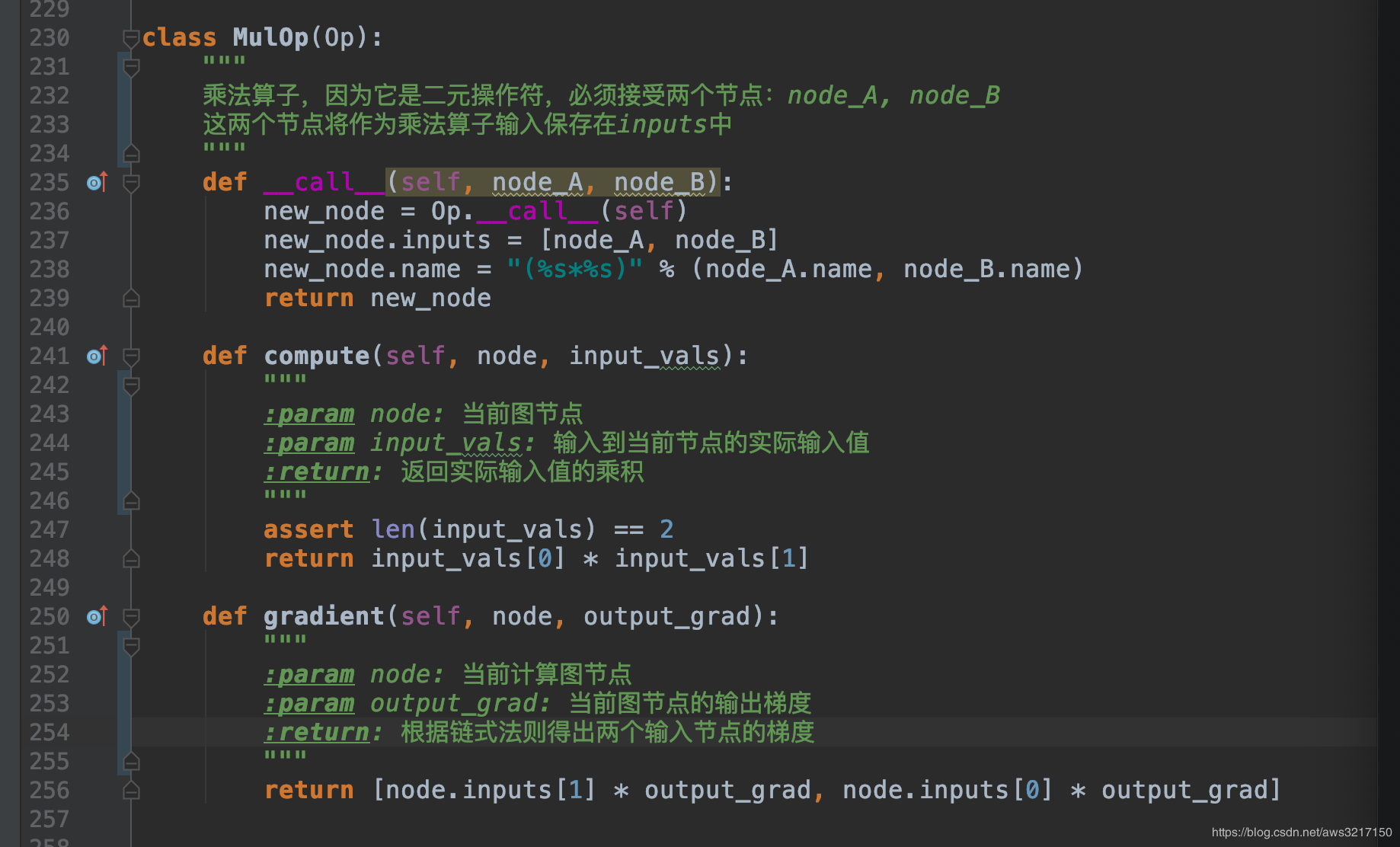
op实现了对应梯度的计算方法