1. 前言

本文的目的，是引导新入职同事快速融入环境，掌握足够的基础知识，尽快开展工作的第一份指导文件。

2. 深度学习

相信大家都听说过人工智能（Artificial Intelligence，简称AI），但什么是AI？它有什么作用，研究方向有哪些，涉及到哪些技术？大家一定有数不清的问题要问，下面我将逐一回答。

2.1 AI定义

==人工智能是让机器获得像人类一样具有思考和推理机制的智能技术==，这一概念最早出现在1956 年召开的达特茅斯会议上。这是一项极具挑战性的任务，人类目前尚无法对人脑的工作机制有全面、科学的认知，希望能制造达到人脑水平的智能机器无疑是难于上青天。即使如此，在某个方面呈现出类似、接近甚至超越人类智能水平的机器被证明是可行的。

信息技术是人类历史上的第三次工业革命，计算机、互联网、智能家居等技术的普及极大地方便了人们的日常生活。通过编程的方式，人类可以将提前设计好的交互逻辑交给机器重复且快速地执行，从而将人类从简单枯燥的重复劳动工作中解脱出来。但是对于需要较高智能水平的任务，如人脸识别、聊天机器人、自动驾驶等任务，很难设计明确的逻辑规则，传统的编程方式显得力不从心，而人工智能是有望解决此问题的关键技术。

2.2 发展历程

人工智能的发展主要经历过三个阶段，每个阶段都代表了人们从不同的角度尝试实现人工智能的探索足迹。早期，人们试图通过总结、归纳出一些逻辑规则，并将逻辑规则以计算机程序的方式实现，来开发出智能系统。但是这种显式的规则往往过于简单，并且很难表达复杂、抽象的概念和规则。这一阶段被称为推理期。

1970 年代，科学家们尝试通过知识库加推理的方式解决人工智能，通过构建庞大复杂的专家系统来模拟人类专家的智能水平。这些明确指定规则的方式存在一个最大的难题，就是很多复杂、抽象的概念无法用具体的代码实现。比如人类对图片的识别、对语言的理解过程，根本无法通过既定规则模拟。为了解决这类问题，一门通过让机器自动从数据中学习规则的研究学科诞生了，称为机器学习，并在1980 年代成为人工智能中的热门学科。在机器学习中，有一门通过神经网络来学习复杂、抽象逻辑的方向，称为神经网络。

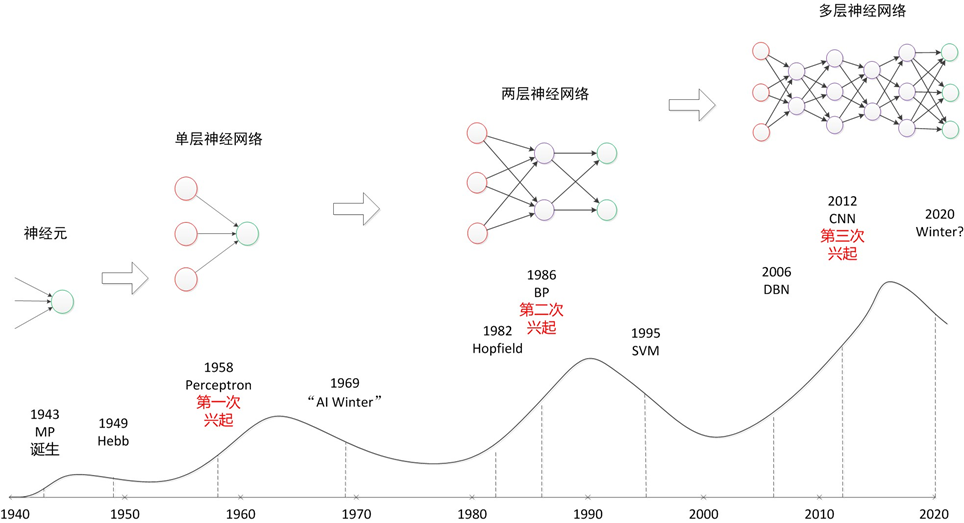
神经网络发展史

神经网络方向的研究经历了两起两落。2012 年开始，由于效果极为显著，应用深层神经网络技术在计算机视觉、自然语言处理、机器人等领域取得了重大突破，部分任务上甚至超越了人类智能水平，开启了以深层神经网络为代表的人工智能的第三次复兴。深层神经网络有了一个新名字，叫作深度学习。一般来讲，神经网络和深度学习的本质区别并不大，深度学习特指基于深层神经网络实现的模型或算法。

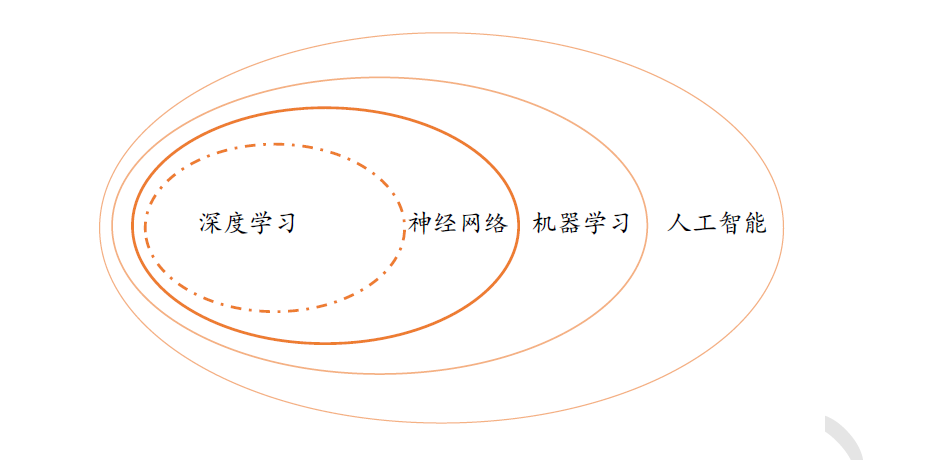
2.3 深度学习算法

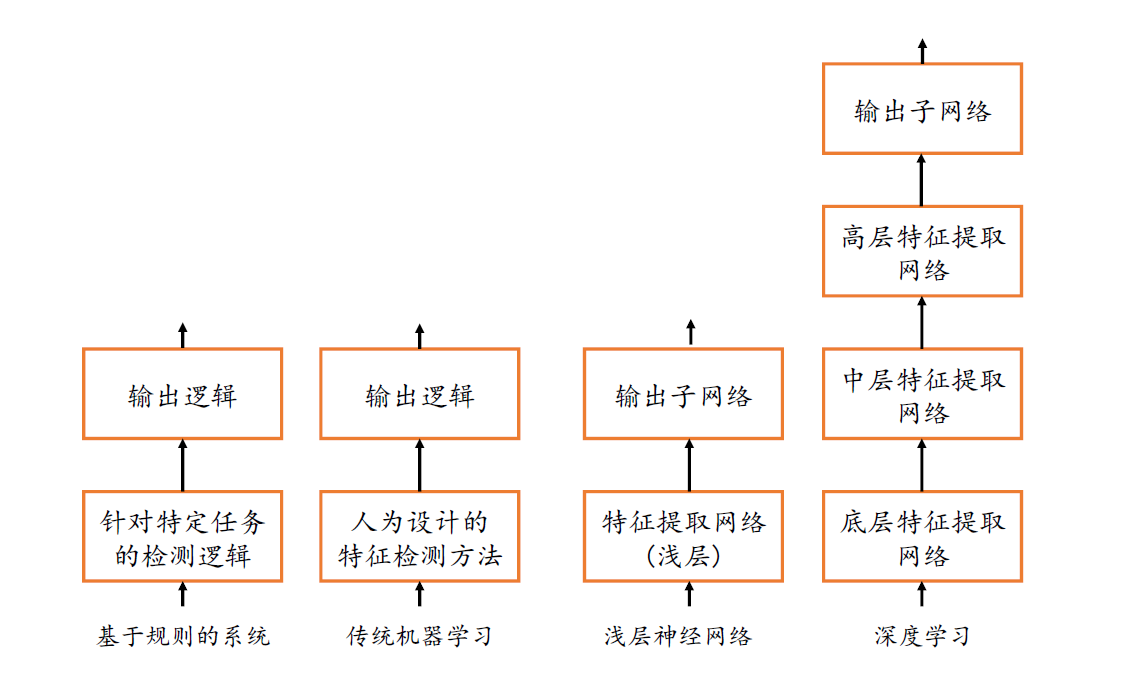
基于规则的系统一般会编写显式的规则逻辑，这些逻辑一般是针对特定的任务设计的，并不适合其他任务。传统的机器学习算法一般会人为设计具有一定通用性的特征检测方法，如SIFT、HOG 特征，这些特征能够适合某一类的任务，具有一定的通用性，但是如何设计特征方法，以及特征方法的优劣性是问题的关键。神经网络的出现，使得人为设计特征这一部分工作可以通过神经网络让机器自动学习完成，不需要人类干预。但是浅层的神经网络的特征提取能力较为有限，而深层的神经网络擅长提取高层、抽象的特征，因此具有更好的性能表现。

2.4 深度学习应用

2.4.1 计算机视觉

图片识别(Image Classification) 是常见的分类问题。神经网络的输入为图片数据，输出值为当前样本属于每个类别的概率分布。通常选取概率值最大的类别作为样本的预测类别。图片识别是最早成功应用深度学习的任务之一，经典的网络模型有VGG 系列、Inception 系列、ResNet 系列等。
目标检测(Object Detection) 是指通过算法自动检测出图片中常见物体的大致位置，通常用边界框(Bounding box)表示，并分类出边界框中物体的类别信息。常见的目标检测算法有RCNN、Fast RCNN、Faster CNN、Mask RCNN、SSD、YOLO 系列等。
语义分割(Semantic Segmentation) 是通过算法自动分割并识别出图片中的内容，可以将语义分割理解为每个像素点的分类问题，分析每个像素点的物体的类别信息。常见的语义分割模型有FCN、U-net、SegNet、DeepLab 系列等。
视频理解(Video Understanding) 随着深度学习在2D 图片的相关任务上取得较好的效果，具有时间维度信息的3D 视频理解任务受到越来越多的关注。常见的视频理解任务有视频分类、行为检测、视频主体抽取等。常用的模型有C3D、TSN、DOVF、TS_LSTM等。
图片生成(Image Generation) 通过学习真实图片的分布，并从学习到的分布中采样而获得逼真度较高的生成图片。目前常见的生成模型有VAE 系列、GAN 系列等。其中GAN 系列算法近年来取得了巨大的进展，最新GAN 模型产生的图片效果达到了肉眼难辨真伪的程度。

2.4.2 自然语言处理

机器翻译(Machine Translation) 过去的机器翻译算法通常是基于统计机器翻译模型，这也是2016 年前Google 翻译系统采用的技术。2016 年11 月，Google 基于Seq2Seq 模型上线了Google 神经机器翻译系统(GNMT)，首次实现了源语言到目标语言的直译技术，在多项任务上获得了50~90%的效果提升。常用的机器翻译模型有Seq2Seq、BERT、GPT、GPT-2 等，其中OpenAI 提出的GPT-2 模型参数量高达15 亿个，甚至发布之初以技术安全考虑为由拒绝开源GPT-2 模型。
聊天机器人(Chatbot) 聊天机器人也是自然语言处理的一项主流任务，机器自动学习与人类对话，对于人类的简单诉求提供满意的自动回复，提高客户的服务效率和服务质量等。常应用在咨询系统、娱乐系统、智能家居等中。

2.4.3 强化学习

虚拟游戏相对于真实环境，虚拟游戏平台既可以训练、测试强化学习算法，又可以避免无关因素干扰，同时也能将实验代价降到最低。目前常用的虚拟游戏平台有OpenAI Gym、OpenAI Universe、OpenAI Roboschool、DeepMind OpenSpiel、MuJoCo 等，常用的强化学习算法有DQN、A3C、A2C、PPO 等。在围棋领域，DeepMind AlaphGo 程序已经超越人类围棋专家；在Dota2 和星际争霸游戏上，OpenAI 和DeepMind 开发的智能程序也在限制规则下战胜了职业队伍。
机器人(Robotics) 在真实环境中，机器人的控制也取得了一定的进展。如UC Berkeley实验室在机器人领域的Imitation Learning、Meta Learning、Few-shot Learning 等方向上取得了不少进展。美国波士顿动力公司在机器人应用中取得喜人的成就，其制造的机器人在复杂地形行走、多智能体协作等任务上表现良好(图 1.19)。
自动驾驶(Autonomous Driving) 被认为是强化学习短期内能技术落地的一个应用方向，很多公司投入大量资源在自动驾驶上，如百度、Uber、Google 无人车等，其中百度的无人巴士“阿波龙”已经在北京、雄安、武汉等地展开试运营。

3. 必备的基础知识

3.1 神经网络

3.1.1 神经元模型

详见 https://www.cnblogs.com/maybe2030/p/5597716.html

生物神经元模型，是现代深度学习的基石。

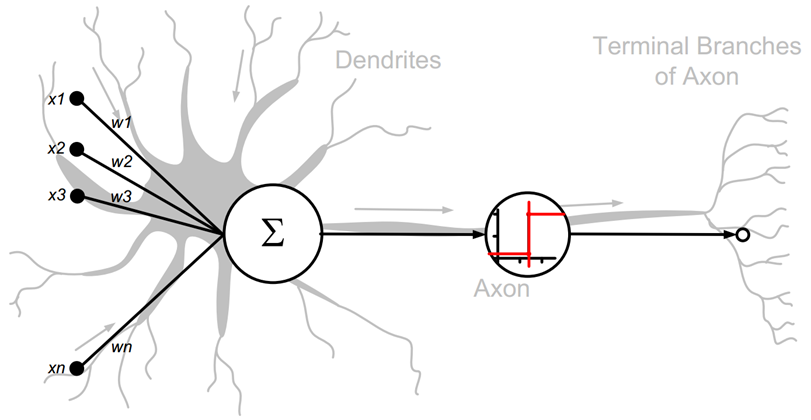
1575616572055

抽象神经元模型

神经网络单元

参数𝜃 = {𝑤1, 𝑤2, 𝑤3, . . . , 𝑤𝑛, 𝑏}确定了神经元的状态，通过固定𝜃参数即可确定此神经元的处理逻辑。当神经元输入节点数𝑛 = 1(单输入)时，神经元数学模型可进一步简化为： 𝑦 = 𝑤𝑥 + 𝑏

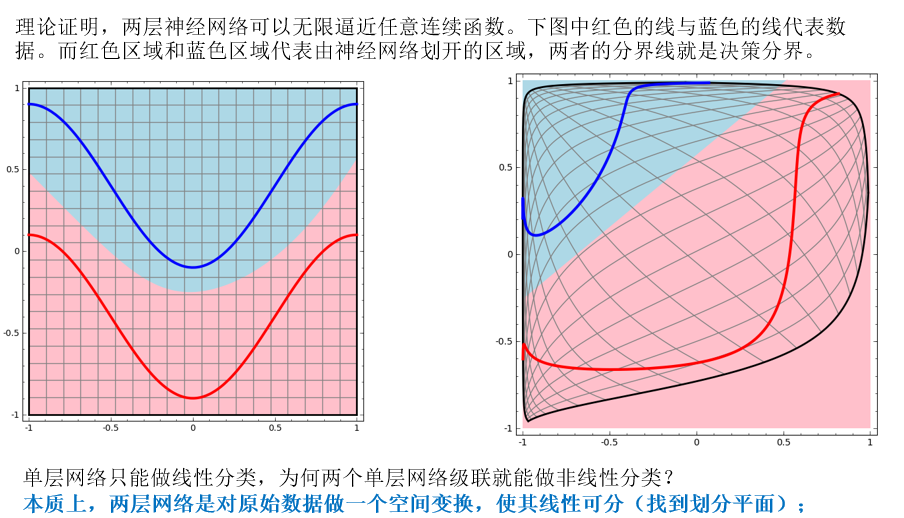
3.1.2 两层神经网络

两层神经网络除了包含一个输入层，一个输出层以外，还增加了一个中间层。此时，中间层和输出层都是计算层。当增加一个计算层以后，两层神经网络不仅可以解决异或问题，而且具有非常好的非线性分类效果。

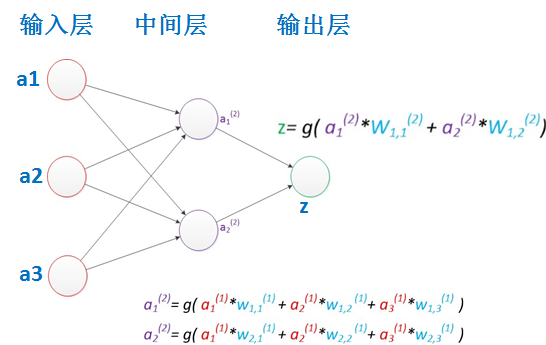
1575617816143

两层网络效果

3.2 python

https://www.runoob.com/python3/python3-tutorial.html

python速查表

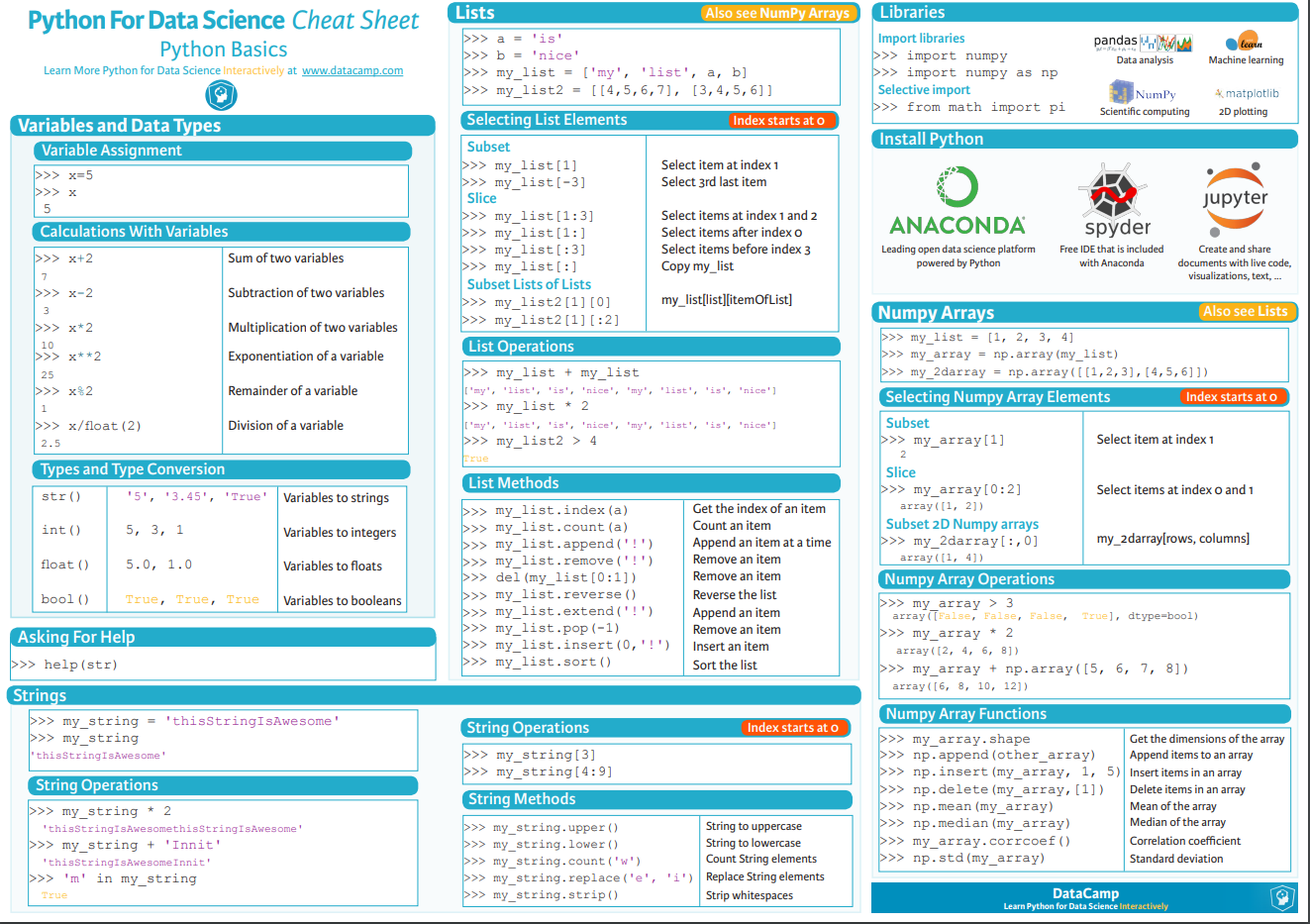
python_quick

3.3 tensorflow

tensorflow是google主导的，目前最火的开源深度学习框架。

速查表：https://aicheatsheets.com/static/pdfs/tensorflow_v_2.0.pdf

API文档：https://www.tensorflow.org/api_docs/python/tf

3.4 caffe/pytorch

caffe是由加州大学伯克利分校的贾扬清博士于2013年在Github上发布的深度学习框架。

caffe2是在2017年4月18日开幕的 F8 年度开发者大会上，Facebook 发布的一款全新的开源深度学习框架，目前已经并入pytorch。

pytorch文档：https://pytorch.org/docs/stable/rpc.html

4. MNN

MNN是一个轻量级的深度神经网络推理引擎，在端侧加载深度神经网络模型进行推理预测。目前，MNN已经在阿里巴巴的手机淘宝、手机天猫、优酷等20多个App中使用，覆盖直播、短视频、搜索推荐、商品图像搜索、互动营销、权益发放、安全风控等场景。此外，IoT等场景下也有若干应用。

==MNN是重点参考对象，需要特别关注。==

4.1 特点

4.1.1 轻量性

针对端侧设备特点深度定制和裁剪，无任何依赖，可以方便地部署到移动设备和各种嵌入式设备中。
iOS平台：armv7+arm64静态库大小5MB左右，链接生成可执行文件增加大小620KB左右，metallib文件600KB左右。
Android平台：so大小400KB左右，OpenCL库400KB左右，Vulkan库400KB左右。

4.1.2 通用性

支持Tensorflow、Caffe、ONNX等主流模型文件格式，支持CNN、RNN、GAN等常用网络。
支持86个TensorflowOp、34个CaffeOp；各计算设备支持的MNN Op数：CPU 71个，Metal 55个，OpenCL 29个，Vulkan 31个。
支持iOS 8.0+、Android 4.3+和具有POSIX接口的嵌入式设备。
支持异构设备混合计算，目前支持CPU和GPU，可以动态导入GPU Op插件，替代CPU Op的实现。

4.1.3 高性能

不依赖任何第三方计算库，依靠大量手写汇编实现核心运算，充分发挥ARM CPU的算力。
iOS设备上可以开启GPU加速（Metal），常用模型上快于苹果原生的CoreML。
Android上提供了OpenCL、Vulkan、OpenGL三套方案，尽可能多地满足设备需求，针对主流GPU（Adreno和Mali）做了深度调优。
卷积、转置卷积算法高效稳定，对于任意形状的卷积均能高效运行，广泛运用了 Winograd 卷积算法，对3x3 -> 7x7之类的对称卷积有高效的实现。
针对ARM v8.2的新架构额外作了优化，新设备可利用半精度计算的特性进一步提速。

4.1.4 易用性

有高效的图像处理模块，覆盖常见的形变、转换等需求，一般情况下，无需额外引入libyuv或opencv库处理图像。
支持回调机制，可以在网络运行中插入回调，提取数据或者控制运行走向。
支持只运行网络中的一部分，或者指定CPU和GPU间并行运行。

4.2 架构

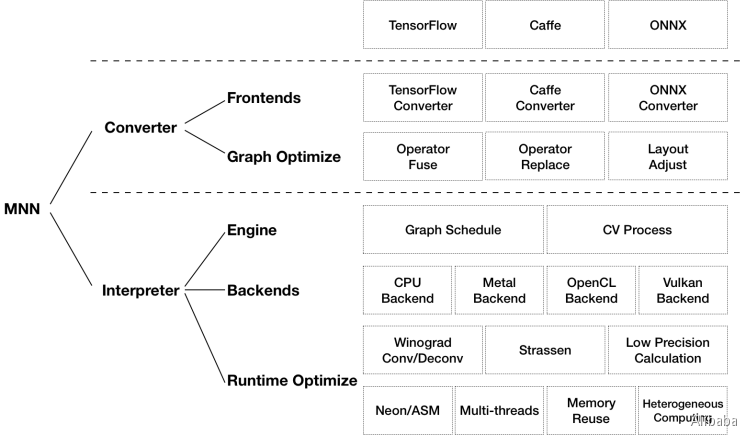
MNN可以分为Converter和Interpreter两部分。

Converter由Frontends和Graph Optimize构成。前者负责支持不同的训练框架，MNN当前支持Tensorflow(Lite)、Caffe和ONNX(PyTorch/MXNet的模型可先转为ONNX模型再转到MNN)；后者通过算子融合、算子替代、布局调整等方式优化图。

Interpreter由Engine和Backends构成。前者负责模型的加载、计算图的调度；后者包含各计算设备下的内存分配、Op实现。在Engine和Backends中，MNN应用了多种优化方案，包括在卷积和反卷积中应用Winograd算法、在矩阵乘法中应用Strassen算法、低精度计算、Neon优化、手写汇编、多线程优化、内存复用、异构计算等。

4.3 用法

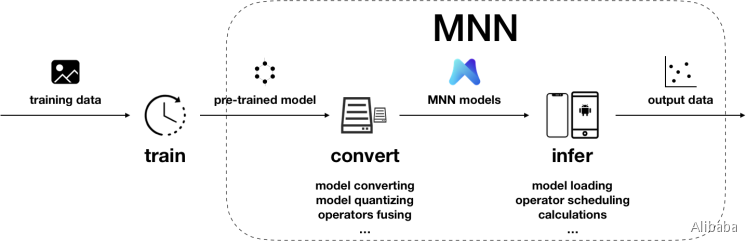
训练

在训练框架上，根据训练数据训练出模型的阶段。虽然当前MNN也提供了训练模型的能力，但主要用于端侧训练或模型调优。在数据量较大时，依然建议使用成熟的训练框架，如TensorFlow、PyTorch等。除了自行训练外，也可以直接利用开源的预训练模型。

转换

将其他训练框架模型转换为MNN模型的阶段。MNN当前支持Tensorflow(Lite)、Caffe和ONNX的模型转换。模型转换工具可以参考编译文档和使用说明。支持转换的算子，可以参考算子列表文档；在遇到不支持的算子时，可以尝试自定义算子，或在Github上给我们提交issue。

此外，模型打印工具可以用于输出模型结构，辅助调试。

除模型转换外，MNN也提供了模型量化工具，可以对浮点模型进行量化压缩。

推理

在端侧加载MNN模型进行推理的阶段。端侧运行库的编译请参考各平台的编译文档：iOS、Android、Linux/macOS/Ubuntu、Windows。我们提供了API接口文档，也详细说明了会话创建、数据输入、执行推理、数据输出相关的接口和参数。

4.4 源码分析

4.4.1 代码路径

内容	作用
3rd_party	第三方工具
benchmark	性能测试工具
cmake	编译相关
CMakeLists.txt	编译相关
demo	demo
doc	文档
express
include	头文件
project	android，ios，linux工程
pymnn	python包
resource	模型，图片等资源
schema	描述文件，编译相关
source	核心算法库
test	测试相关
tools	converter模型转换，quantization量化等工具

重点关注source目录，source下面有5个目录，分别为

目录	用途
backend	CPU，GPU加速后端
core	核心框架，backend，session，pipeline，execution，schedule等框架
cv	图像库，各种颜色格式，图像格式转换，
math	matrix，vertex，wingored基本运算
shape	算子shape计算

4.4.2 backend后端实现

arm82：这个目录下面是arm处理器的优化cpu算子，包含1X1的卷积，矩阵优化汇编等几个优化实现。
cpu：通用的cpu后端实现，包含x86的asm，sse，avx等优化实现
metal：Apple GPU加速方案，只能用于ios， macos，属于底层语言，性能比较好。
opencl， opengl：Khronos开源GPU加速高级API，兼容多种平台，开销较大，逐步被淘汰中。
vulkan：Khronos最新的底层GPU加速API，是AMD mantle的后续版本，未来的趋势。

4.5 总结

==算子分析关注source/shape，source/backend目录即可。==

5. CPU算子分析

所谓的算子，其实就是某种运算，例如常见的加减乘除，平方，开根号等操作，当然，这些比较简单，也有复杂的，例如卷积。

算子的功能各异，命名也没有统一标准，我们需要了解不同框架的实现细节，才能更精确地在IR中定义并实现，大致来讲，拿到一个算子，我们可以按照下述步骤来分析。

在这里我们以exp算子为例，讲述分析过程，其他算子类似。

5.1 算子定义

对于算子定义，我们定义一个模板，第一步就是弄清楚算子的功能和输入输出

类型	功能描述	输入参数	输出参数	返回值	注意事项
MNN定义
tensorflow定义
caffe/pytorch定义

mnn定义可以去https://www.yuque.com/mnn/en/ops搜索算子名称exp

由MNN文档可以看出，tensorflow的exp算子，MNN和caffe是用UnaryOp实现的，UnaryOp其实支持好几种类型的运算：rsqrt，square，neg，exp，sqrt等，是个大的集合，输入输出对象都是是float32类型的浮点数，数据支持NHWC或者NCHW存贮格式。

接下来，我们去tensorflow文档 https://www.tensorflow.org/api_docs/python/tf 里面搜索exp，可以找到

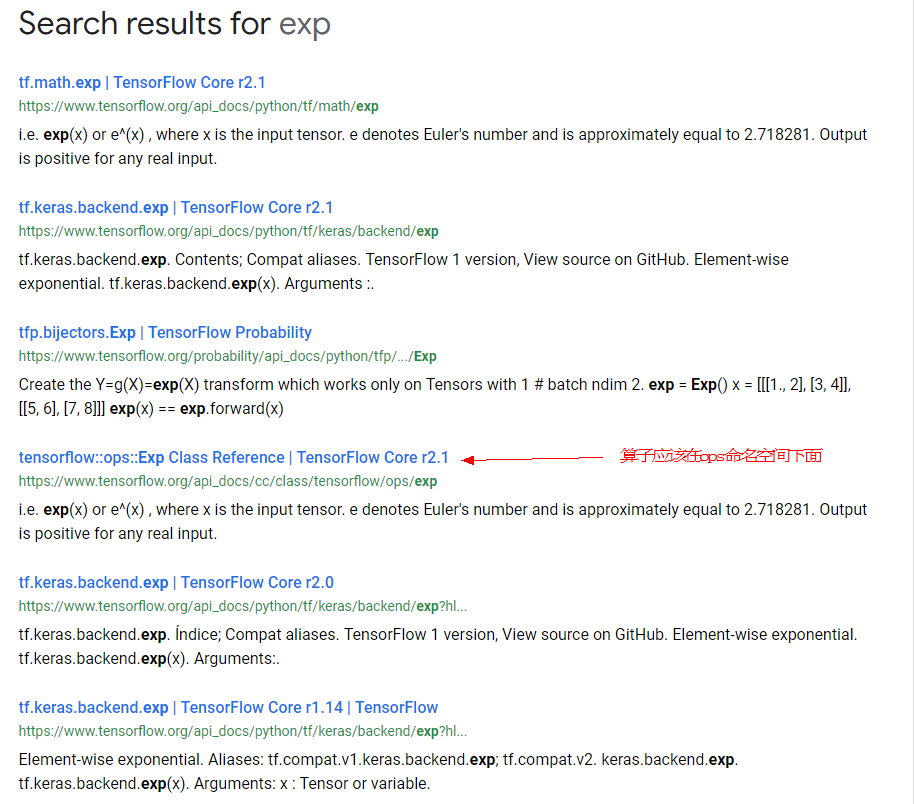
跳转tensorflow::ops::Exp的定义，我们能看到tensorflow对该算子的定义，功能描述及使用例子。重点部分见代码中文注释，以下类同。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34


#include <math_ops.h> # 说明用math命名空间的实现

Computes exponential of x element-wise.

Summary
\(y = e^x\).

This function computes the exponential of every element in the input tensor. i.e. exp(x) or e^(x), where x is the input tensor. e denotes Euler's number and is approximately equal to 2.718281. Output is positive for any real input.


  # 使用例子

  x = tf.constant(2.0)
  tf.math.exp(x) ==> 7.389056

  x = tf.constant([2.0, 8.0])
  tf.math.exp(x) ==> array([7.389056, 2980.958], dtype=float32)
  

# 复数计算公式

For complex numbers, the exponential value is calculated as follows:

  e^(x+iy) = e^x * e^iy = e^x * (cos y + i sin y)
  

Let's consider complex number 1+1j as an example. e^1 * (cos 1 + i sin 1) = 2.7182818284590 * (0.54030230586+0.8414709848j)


  x = tf.constant(1 + 1j)
  tf.math.exp(x) ==> 1.4686939399158851+2.2873552871788423j
  

Arguments:

scope: A Scope object
Returns:

Output: The y tensor.

从该文档可以看出，exp算子是计算输入的e指数。 $$ y

e ^x $$ 这个算子需要包含math_ops.h，说明它是靠tensorflow::math下面的函数实现的，我们继续跳转到tf.math.exp的文档

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37


Computes exponential of x element-wise. .

Aliases: tf.exp

tf.math.exp(
    x,
    name=None
)

Used in the guide:
Writing custom layers and models with Keras
Eager execution
Used in the tutorials:
Convolutional Variational Autoencoder

This function computes the exponential of every element in the input tensor. i.e. exp(x) or e^(x), where x is the input tensor. e denotes Euler's number and is approximately equal to 2.718281. Output is positive for any real input.


x = tf.constant(2.0)
tf.math.exp(x) ==> 7.389056

x = tf.constant([2.0, 8.0])
tf.math.exp(x) ==> array([7.389056, 2980.958], dtype=float32)

For complex numbers, the exponential value is calculated as follows:

e^(x+iy) = e^x * e^iy = e^x * (cos y + i sin y)

Let's consider complex number 1+1j as an example. e^1 * (cos 1 + i sin 1) = 2.7182818284590 * (0.54030230586+0.8414709848j)


x = tf.constant(1 + 1j)
tf.math.exp(x) ==> 1.4686939399158851+2.2873552871788423j

Args:
x: A Tensor. Must be one of the following types: bfloat16, half, float32, float64, complex64, complex128.
name: A name for the operation (optional).
Returns:
A Tensor. Has the same type as x.

重点关注输入输出，发现类型输入输入tensor类型一致，输入支持bfloat16, half, float32, float64, complex64, complex128.

最后，我们去https://pytorch.org/docs/stable/rpc.html搜索pytorch关于exp的定义，跳转到toych.exp

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


torch.exp(input, out=None) → Tensor
Returns a new tensor with the exponential of the elements of the input tensor input.

y_{i} = e^{x_{i}}
y 
i
​	
 =e 
x 
i
​	
 
 
Parameters
input (Tensor) – the input tensor.

out (Tensor, optional) – the output tensor.

Example:

>>> torch.exp(torch.tensor([0, math.log(2.)]))
tensor([ 1.,  2.])

pytorch的文档只是指出了exp是做什么用的，对输入输出并没有特别的描述。没办法，只能去看代码，在pytorch里面搜索exp，找到caffe2/operators/exp_op.cc，能看到要求输入输出为1个，且类型，shape相同。输入输出为float类型。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80


REGISTER_CPU_OPERATOR(
    Exp,
    UnaryElementwiseOp<TensorTypes<float>, CPUContext, ExpFunctor<CPUContext>>);

OPERATOR_SCHEMA(Exp)
    .NumInputs(1)  // 一个输入
    .NumOutputs(1) // 一个输出
    .AllowInplace({{0, 0}})
    .IdenticalTypeAndShape()  // 类型，shape需要相同
    .SetDoc(R"DOC(

Calculates the exponential of the given input tensor ($exp(x)$), element-wise. This
operation can be done in an in-place fashion too, by providing the same input
and output blobs.

Github Link:
- https://github.com/pytorch/pytorch/blob/master/caffe2/operators/exp_op.cc

<details>

<summary> <b>Example</b> </summary>

**Code**

```

workspace.ResetWorkspace()

op = core.CreateOperator(
    "Exp",
    ["X"],
    ["X"],
)

workspace.FeedBlob("X", (np.random.rand(3,3)).astype(np.float32))
print("X before running op:", workspace.FetchBlob("X"))
workspace.RunOperatorOnce(op)
print("X after running op:", workspace.FetchBlob("X"))

```

**Result**

```

X before running op:
[[0.5821691  0.07719802 0.50159824]
 [0.40952456 0.36788362 0.84887683]
 [0.02472685 0.65730894 0.9066397 ]]
X after running op:
[[1.7899168 1.080256  1.6513585]
 [1.5061016 1.4446739 2.3370204]
 [1.0250351 1.9295927 2.4759884]]

```

</details>

)DOC")

    .Input(0, "X", "*(type: Tensor`<float>`)* Input tensor.")  // 输入为float类型
    .Output(              // 输出也为float类型
        0,
        "Y",
        "*(type: Tensor`<float>`)* The exponential of the input tensor computed "
        "element-wise.")
    .InheritOnnxSchema();

namespace {

class GetExpGradient : public GradientMakerBase {
  using GradientMakerBase::GradientMakerBase;
  std::vector<OperatorDef> GetGradientDefs() override {
    return SingleGradientDef(
        "Mul",
        "",
        std::vector<std::string>{O(0), GO(0)},
        std::vector<std::string>{GI(0)});
  }
};

} // namespace

caffe/pytorch文档确实没有tensorflow完整，可能需要去看源码才能知道有什么约束。

综上分析，我们可以整理出来算子定义的表格，对算子的功能及约束就心里有数了。

类型	功能描述	输入参数	输出参数	注意事项
MNN定义	计算e指数	float32	float32
tensorflow定义	计算e指数	bfloat16, half, float32, float64, complex64, complex128	bfloat16, half, float32, float64, complex64, complex128	输入输出类型，shape一样
caffe/pytorch定义	计算e指数	float	float	输入输出类型，shape一样

5.2 MNN实现分析

从上节知道MNN中exp算子是由unary算子实现的，本节我们将看MNN的代码实现。首先去MNN代码树source/shape下面搜索有unary子串的文件，或者直接搜索算子名字OpType_UnaryOp。对exp算子而言，搜索不到任何信息，因为exp算子比较简单，输入输出的shape是一样的，无需改变，所以没有特别的实现。

这块我们用另外一个算子cast来解释，cast算子其实就是高级语言里面的类型转换，例如int转换为float格式。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30


class CastSizeComputer : public SizeComputer {
public:
    // onComputeSize虚函数更新tensor参数信息
    virtual bool onComputeSize(const MNN::Op* op, const std::vector<Tensor*>& inputs,
                               const std::vector<Tensor*>& outputs) const override {
        auto output = outputs[0];
        auto input  = inputs[0];
        TensorUtils::copyShape(input, output, true);
        // float -> int8情况，输出类型需要改为int8类型
        if (OpType_FloatToInt8 == op->type()) {
            output->buffer().type = halide_type_of<int8_t>();
            return true;
        }
        // int8 -> float情况，输出类型需要改为float类型
        if (OpType_Int8ToFloat == op->type()) {
            output->buffer().type = halide_type_of<float>();
            return true;
        }

        const auto opParam = op->main_as_CastParam();
        // 通用类型转换，输出设置为dest类型
        outputs[0]->setType(opParam->dstT());

        return true;
    }
};
// CastSizeComputer算子其实注册了3种类型的转换，cast， float -> int8, int8 -> float
REGISTER_SHAPE(CastSizeComputer, OpType_Cast);
REGISTER_SHAPE(CastSizeComputer, OpType_FloatToInt8);
REGISTER_SHAPE(CastSizeComputer, OpType_Int8ToFloat);

如果算子的shape大小发生变化，这里也需要设置好。

有了算子的shape，类型信息，我们再回到exp算子的实现代码，这回在source/backend/cpu下面搜索OpType_UnaryOp，我们可以找到source/backend/cpu/CPUUnary.cpp，这个文件其实就是借用C++模板实现了逐个元素计算单目操作符exp之类的算子，代码其实很简单，重点部分请参见中文注释。

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435



namespace MNN {
CPUUnary::CPUUnary(Backend *b, UnaryOpOperation type) : MNN::Execution(b), mType(type) {
    // nothing to do
}

ErrorCode CPUUnary::onResize(const std::vector<Tensor *> &inputs, const std::vector<Tensor *> &outputs) {
    MNN_ASSERT(1 == outputs.size());
    auto dtype = inputs[0]->getType();
    MNN_ASSERT(dtype == halide_type_of<float>() || dtype == halide_type_of<int32_t>());
    return NO_ERROR;
}

// 逐元素计算函数f
template <typename Func, typename T>
static ErrorCode _unaryOp(Tensor *input, Tensor *output) {
    Func f;

    const T *inputData = input->host<T>();
    T *outputData      = (T *)output->buffer().host;

    auto elementSize = input->elementSize();

    for (int i = 0; i < elementSize; i++) {
        outputData[i] = f(inputData[i]);
    }

    return NO_ERROR;
}

template <typename T>
struct UnarySquare : std::unary_function<T, T> {
    T operator()(const T &x) const {
        return x * x;
    }
};

template <typename T>
struct UnaryRsqrt : std::unary_function<T, T> {
    T operator()(const T &x) const {
        return 1.f / sqrt(x);
    }
};

template <typename T>
struct UnarySqrt : std::unary_function<T, T> {
    T operator()(const T &x) const {
        return sqrt(x);
    }
};

template <typename T>
struct UnaryNeg {
    T operator()(const T &x) const {
        return -x;
    }
};
// exp算子计算模板
template <typename T>
struct UnaryExp : std::unary_function<T, T> {
    T operator()(const T &x) const {
        return exp(x);
    }
};

template <typename T>
struct UnaryAbs : std::unary_function<T, T> {
    T operator()(const T &x) const {
        return abs(x);
    }
};

template <typename T>
struct UnaryCeil : std::unary_function<T, T> {
    T operator()(const T &x) const {
        return ceil(x);
    }
};
template <typename T>
struct UnaryRecipocal : std::unary_function<T, T> {
    T operator()(const T &x) const {
        return (T)1 / (x);
    }
};
template <typename T>
struct UnaryLog1p : std::unary_function<T, T> {
    T operator()(const T &x) const {
        return (T)log((T)1 + (x));
    }
};
template <typename T>
struct UnaryLog : std::unary_function<T, T> {
    T operator()(const T &x) const {
        return (T)log((T)(x));
    }
};
template <typename T>
struct UnaryCos : std::unary_function<T, T> {
    T operator()(const T &x) const {
        return (T)cosf((T)(x));
    }
};
template <typename T>
struct UnarySin : std::unary_function<T, T> {
    T operator()(const T &x) const {
        return (T)sinf((T)(x));
    }
};
template <typename T>
struct UnaryTan : std::unary_function<T, T> {
    T operator()(const T &x) const {
        return (T)tanf((T)(x));
    }
};
template <typename T>
struct UnaryATan : std::unary_function<T, T> {
    T operator()(const T &x) const {
        return (T)atanf((T)(x));
    }
};

template <typename T>
struct UnaryFloor : std::unary_function<T, T> {
    T operator()(const T &x) const {
        return (T)floor((T)(x));
    }
};

template <typename T>
struct UnarySign : std::unary_function<T, T> {
    T operator()(const T &x) const {
        if (x > 0) {
            return 1;
        }
        if (x < 0) {
            return -1;
        }
        return 0;
    }
};

template <typename T>
struct UnaryBNLL : std::unary_function<T, T> {
    T operator()(const T &x) const {
        float r = x > 0 ? (x + log(1. + exp(-x))) : log(1. + exp(x));
        return (T)r;
    }
};

template <typename T>
struct UnaryAcosh : std::unary_function<T, T> {
    T operator()(const T &x) const {
        return (T)acoshf((T)(x));
    }
};

template <typename T>
struct UnarySinh : std::unary_function<T, T> {
    T operator()(const T &x) const {
        return (T)sinhf((T)(x));
    }
};

template <typename T>
struct UnaryAsinh : std::unary_function<T, T> {
    T operator()(const T &x) const {
        return (T)asinhf((T)(x));
    }
};

template <typename T>
struct UnaryAtanh : std::unary_function<T, T> {
    T operator()(const T &x) const {
        return (T)atanhf((T)(x));
    }
};
template <typename T>
struct UnaryRound : std::unary_function<T, T> {
    T operator()(const T &x) const {
        return (T)roundf((T)(x));
    }
};

template <typename T>
struct UnaryCosh : std::unary_function<T, T> {
    T operator()(const T &x) const {
        return (T)coshf((T)(x));
    }
};

template <typename T>
T evalPoly(T x, const std::vector<float> kErfTCoefficient) {
    auto poly = 0.0f;
    for (auto c : kErfTCoefficient) {
        poly = poly * x + c;
    }
    return poly;
}

template <typename T>
T erfImpl(T x) {
    // Coefficients for by erf(f32), from Cephes. tensorflow
    static const std::vector<float> kErfTCoefficient {
            +7.853861353153693E-5, -8.010193625184903E-4, +5.188327685732524E-3,
            -2.685381193529856E-2, +1.128358514861418E-1, -3.761262582423300E-1,
            +1.128379165726710E+0,
    };
    return x * evalPoly(x * x, kErfTCoefficient);
}

template <typename T>
T erfcImpl(T x) {
    // Coefficients for erfc(f32), from Cephes. tensorflow
    const double kMaxlog = 88.72283905206835;
    // erfc(x) = exp(-x^2) P(1/x^2), 1 < x < 2
    static const std::vector<float> kErfcPCoefficient{
            +2.326819970068386E-2, -1.387039388740657E-1, +3.687424674597105E-1,
            -5.824733027278666E-1, +6.210004621745983E-1, -4.944515323274145E-1,
            +3.404879937665872E-1, -2.741127028184656E-1, +5.638259427386472E-1,
    };
    // erfc(x) = exp(-x^2) R(1/x^2), 2 <= x < kMaxlog
    static const std::vector<float> kErfcRCoefficient{
            -1.047766399936249E+1, +1.297719955372516E+1, -7.495518717768503E+0,
            +2.921019019210786E+0, -1.015265279202700E+0, +4.218463358204948E-1,
            -2.820767439740514E-1, +5.641895067754075E-1,
    };
    float absX = fabsf(x);
    float z = expf(-x * x);
    float q = 1.0 / absX;
    float y = q * q;
    float p;
    if (absX < 2.0f) {
        p = evalPoly(y, kErfcPCoefficient);
    } else {
        p = evalPoly(y, kErfcRCoefficient);
    }
    y = z * q * p;
    float yClamp;
    if (z < -kMaxlog) {
        yClamp = 0.0f;
    } else {
        yClamp = y;
    }
    if (x < 0) {
        return T(2.0f - yClamp);
    } else {
        return T(yClamp);
    }
}

template <typename T>
struct UnaryErf : std::unary_function<T, T> {
    T operator()(const T &x) const {
        if (abs(x) < T(1.)) {
            return erfImpl(x);
        } else {
            return T(1.) - erfcImpl(x);
        }
    }
};

template <typename T>
struct UnaryErfc : std::unary_function<T, T> {
    T operator()(const T &x) const {
        if (abs(x) > T(1.)) {
            return erfcImpl(x);
        } else {
            return T(1.) - erfImpl(x);
        }
    }
};

template <typename T>
struct UnaryErfinv : std::unary_function<T, T> {
    // referenced from tensorflow
    const int kDegree = 9;
    const std::vector<float> w_less_than_5_constants = {
            2.81022636e-08f,  3.43273939e-07f, -3.5233877e-06f,
            -4.39150654e-06f, 0.00021858087f,  -0.00125372503f,
            -0.00417768164f,  0.246640727f,    1.50140941f};
    const std::vector<float> w_greater_than_5_constants = {
            -0.000200214257f, 0.000100950558f, 0.00134934322f,
            -0.00367342844f,  0.00573950773f,  -0.0076224613f,
            0.00943887047f,   1.00167406f,     2.83297682f};

    T operator()(const T &x) const {
        // Compute logarithm of (1+arg) using log1p(arg) which is more precise than
        // log(1+arg) when arg is close to zero. For more details, see
        // https://en.cppreference.com/w/cpp/numeric/math/log1p
        auto w = -log1p(-x * x);
        bool lt = (w < 5.0);
        auto coefficient = [&](int i) {
            if (lt) {
                return w_less_than_5_constants[i];
            } else {
                return w_greater_than_5_constants[i];
            }
        };
        if (lt) {
            w = w - 2.5;
        } else {
            w = sqrt(w) - 3.0;
        }
        auto p = coefficient(0);
        for (int i = 1; i < kDegree; i++) {
            p = coefficient(i) + p * w;
        }
        auto result = p * x;
        if (fabsf(fabsf(x) - 1) < 1e-8) {
            return std::numeric_limits<float>::infinity();
        } else {
            return result;
        }
    }
};

template <typename T>
struct UnaryExpm1 : std::unary_function<T, T> {
    T operator()(const T &x) const {
        return (T)expm1((T)(x));
    }
};

template <typename T>
struct UnaryAsin : std::unary_function<T, T> {
    T operator()(const T &x) const {
        return (T)asin((T)(x));
    }
};

template <typename T>
struct UnaryAcos : std::unary_function<T, T> {
    T operator()(const T &x) const {
        return (T)acos((T)(x));
    }
};

// 算子计算函数
ErrorCode CPUUnary::onExecute(const std::vector<Tensor *> &inputs, const std::vector<Tensor *> &outputs) {
    auto input  = inputs[0];
    auto output = outputs[0];
    auto dtype  = input->getType().code;

    if (dtype == halide_type_int) {
        switch (mType) {
            case UnaryOpOperation_ABS:
                return _unaryOp<UnaryAbs<int32_t>, int32_t>(input, output);
            case UnaryOpOperation_NEG:
                return _unaryOp<UnaryNeg<int32_t>, int32_t>(input, output);
            case UnaryOpOperation_SQUARE:
                return _unaryOp<UnarySquare<int32_t>, int32_t>(input, output);
            default:
                MNN_ERROR("Int-Unary not support %d\n", mType);
                break;
        }
        return NO_ERROR;
    }
    switch (mType) {
        case UnaryOpOperation_SQUARE:
            return _unaryOp<UnarySquare<float>, float>(input, output);
        case UnaryOpOperation_RSQRT:
            return _unaryOp<UnaryRsqrt<float>, float>(input, output);
        case UnaryOpOperation_NEG:
            return _unaryOp<UnaryNeg<float>, float>(input, output);
        // exp类型的算子，把UnaryExp当做模板参数传给模板函数实现计算
        case UnaryOpOperation_EXP:
            return _unaryOp<UnaryExp<float>, float>(input, output);
        case UnaryOpOperation_COS:
            return _unaryOp<UnaryCos<float>, float>(input, output);
        case UnaryOpOperation_SIN:
            return _unaryOp<UnarySin<float>, float>(input, output);
        case UnaryOpOperation_TAN:
            return _unaryOp<UnaryTan<float>, float>(input, output);
        case UnaryOpOperation_ATAN:
            return _unaryOp<UnaryATan<float>, float>(input, output);
        case UnaryOpOperation_SQRT:
            return _unaryOp<UnarySqrt<float>, float>(input, output);
        case UnaryOpOperation_ABS:
            return _unaryOp<UnaryAbs<float>, float>(input, output);
        case UnaryOpOperation_CEIL:
            return _unaryOp<UnaryCeil<float>, float>(input, output);
        case UnaryOpOperation_RECIPROCAL:
            return _unaryOp<UnaryRecipocal<float>, float>(input, output);
        case UnaryOpOperation_LOG1P:
            return _unaryOp<UnaryLog1p<float>, float>(input, output);
        case UnaryOpOperation_LOG:
            return _unaryOp<UnaryLog<float>, float>(input, output);
        case UnaryOpOperation_FLOOR:
            return _unaryOp<UnaryFloor<float>, float>(input, output);
        case UnaryOpOperation_BNLL:
            return _unaryOp<UnaryBNLL<float>, float>(input, output);
        case UnaryOpOperation_ACOSH:
            return _unaryOp<UnaryAcosh<float>, float>(input, output);
        case UnaryOpOperation_SINH:
            return _unaryOp<UnarySinh<float>, float>(input, output);
        case UnaryOpOperation_ASINH:
            return _unaryOp<UnaryAsinh<float>, float>(input, output);
        case UnaryOpOperation_ATANH:
            return _unaryOp<UnaryAtanh<float>, float>(input, output);
        case UnaryOpOperation_SIGN:
            return _unaryOp<UnarySign<float>, float>(input, output);
        case UnaryOpOperation_ROUND:
            return _unaryOp<UnaryRound<float>, float>(input, output);
        case UnaryOpOperation_COSH:
            return _unaryOp<UnaryCosh<float>, float>(input, output);
        case UnaryOpOperation_ERF:
            return _unaryOp<UnaryErf<float>, float>(input, output);
        case UnaryOpOperation_ERFC:
            return _unaryOp<UnaryErfc<float>, float>(input, output);
        case UnaryOpOperation_ERFINV:
            return _unaryOp<UnaryErfinv<float>, float>(input, output);
        case UnaryOpOperation_EXPM1:
            return _unaryOp<UnaryExpm1<float>, float>(input, output);
        case UnaryOpOperation_ASIN:
            return _unaryOp<UnaryAsin<float>, float>(input, output);
        case UnaryOpOperation_ACOS:
            return _unaryOp<UnaryAcos<float>, float>(input, output);
        default:
            MNN_ASSERT(false);
            break;
    }

    return NO_ERROR;
}

class CPUUnaryCreator : public CPUBackend::Creator {
public:
    virtual Execution *onCreate(const std::vector<Tensor *> &inputs, const std::vector<Tensor *> &outputs,
                                const MNN::Op *op, Backend *backend) const override {
        // 创建算子
        return new CPUUnary(backend, op->main_as_UnaryOp()->opType());
    }
};

REGISTER_CPU_OP_CREATOR(CPUUnaryCreator, OpType_UnaryOp);

5.3 IR接口分析

上节已经了解了MNN的实现，本节评估IR接口定义是否合理，是否存在需要改进的地方

首先，去include/graph/op/math_defs.h搜索exp，得到

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


/*
 * Computes exponential of 'x' element-wise. y = e^x
 * <Input>
 *    x : Input tensor
 * <Output>
 *    y : Output tensor
 * <Added in HiAI version>
 *    100.310.010.013
 */
REG_OP(Exp)
.INPUT(x, TensorType({ DT_FLOAT, DT_DOUBLE}))
.OUTPUT(y, TensorType({ DT_FLOAT, DT_DOUBLE}))
.OP_END()

可见IR对exp的定义也是float，double浮点类型，一个输入，一个输出，不存在问题

5.4 加速情况分析

标准的cpu算子可能存在arm neon，x86 SSE， AVX等多种优化方式，需要看算子实现中是否依赖了MNN下述目录中的函数

1
2
3


source/backend/arm82/
source/backend/cpu/arm
source/backend/cpu/x86_x64

6. GPU算子分析

MNN支持GPU加速，存在metal， Opengl， opencl， vulkan几个后端，他们的地位和CPU相同，但在支持的算子数目，输入输出，类型上存在一定的差异，需要逐个分析，相信大家有了CPU算子分析的经验，可以类推到GPU算子上，本文就不深入展开了。

如何做CPU算子分析

文章目录